Simple Plot of Vector

Question

I have a vector $<x(t),y(t),z(t)>$ constrained to a unit sphere. I am trying to plot what the vector looks like as time progresses. What would be the easiest approach to visualizing this?

I have

x[t_, α_] := -1/Sqrt[1 + α^2]  Sin[ t Sqrt[1 + α^2]]
y[t_, α_] := -α/(1 + α^2) (Cos[t Sqrt[1 + α^2]] - 1)
z[t_, α_] := -1 - (1 - Cos[t Sqrt[1 + α^2]])/(1 + α^2)

I want to plot the vector as a function of t [0,10] and I guess alpha=1.

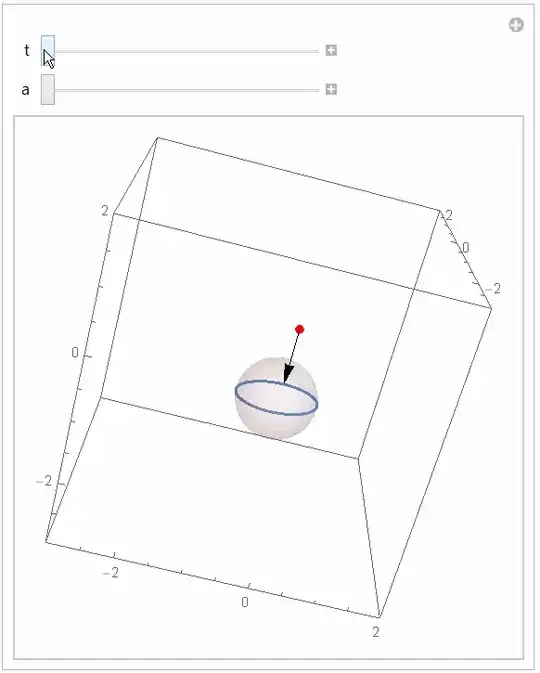
@yankeefan11 You should use = rather than := when possible. In this case nothing needs to be delayed (:= is named "SetDelayed"). — Coolwater, Oct 12 '14 at 06:22
Related: Finding unit tangent, normal, and binormal vectors for a given r(t) — Artes, Oct 12 '14 at 08:46

score 7 · Accepted Answer · answered Oct 12 '14 at 06:03

7

Manipulate[Show[Graphics3D[{
    {Red, PointSize[0.02], Point[{{0, 0, 0}}]},
    {Opacity[0.2], 
     Sphere[{0, a/(1 + a^2), -1 - 1/(1 + a^2)}, 1/Sqrt[1 + a^2]]}, 
    Arrow[{{0, 0, 0}, {x[t, a], y[t, a], z[t, a]}}]}], 
  ParametricPlot3D[{x[u, a], y[u, a], z[u, a]}, {u, 0, 10}], 
  Axes -> True, PlotRange -> Table[{-3, 2}, {3}]], {t, 0, 10}, {a, 1, 
  4}]

enter image description here

answered Oct 12 '14 at 06:03

ubpdqn

60,617
3
59
148

1

Did you generate that gif using just mathematica? – Coolwater Oct 12 '14 at 06:26
1

@Coolwater LICECap software to screen capture – ubpdqn Oct 12 '14 at 07:42

paw · Answer 2 · 2014-10-12T06:06:49.777

5

You can use ParametricPlot3D for this kind of plot. Use Graphics3D if you want to visualize the sphere too.

Show[
 ParametricPlot3D[{x[t, 1], y[t, 1], z[t, 1]}, {t, 0, 10}, 
  PlotStyle -> {Red, Thick}, PlotRangePadding -> 0.31],
 Graphics3D[{Opacity[0.5], Sphere[{0.0, 0.5, -1.5}, 1/Sqrt[2]]}]
 ]

enter image description here

edited Oct 12 '14 at 06:06

answered Oct 12 '14 at 05:55

paw

5,650
23
31

Simple Plot of Vector

2 Answers2