Sequence generation

Question

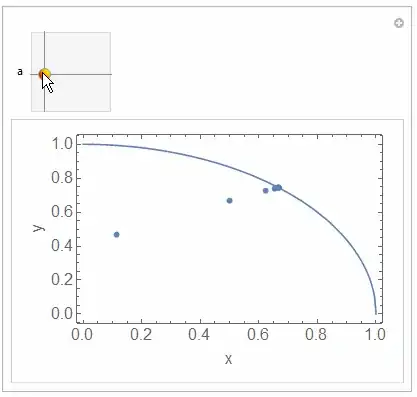
If I wanted to generate a sequence that follows the pattern

$$x_{n}=x_{n-1}+\dfrac{1}{2}\left(\sqrt{1-y_{n-1}\ ^{2}}-x_{n-1}\right)\\ y_{n}=y_{n-1}+\dfrac{1}{2}\left(\sqrt{1-x_{n}\ ^{2}}-y_{n-1}\right)$$

rather than writing the whole thing out:

x0 = N[0 + 1/2 (Sqrt[1 - 0^2] - 0)];
y0 = N[0 + 1/2 (Sqrt[1 - x0^2] - 0)];
x1 = N[x0 + 1/2 (Sqrt[1 - y0^2] - x0)];
y1 = N[y0 + 1/2 (Sqrt[1 - x1^2] - y0)];

... etc. What is the best way to do it?

Stelios · Accepted Answer · 2014-10-12T21:16:27.327

The previous answers correspond to the recursive model of the form $$[x_n,y_n]=[f(x_{n-1},y_{n-1}),g(x_{n-1},y_{n-1})]$$. However, the state-space model of the question is of the form \begin{align} [x_n,y_n]&=[f(x_{n-1},y_{n-1}),g(x_{n-1},y_{n-1},x_n)]\\ &=[f(x_{n-1},y_{n-1}),g(x_{n-1},y_{n-1},f(x_{n-1},y_{n-1}))] \end{align} The latter equation is the correct form that should be applied with the methods proposed by the previous answers. Another method could be to use NestList

h[{x_, y_}] := {x + 1/2 (Sqrt[1 - y^2] - x), 
   y + 1/2 (Sqrt[1 - (x + 1/2 (Sqrt[1 - y^2] - x))^2] - y)};
x0 = N[0 + 1/2 (Sqrt[1 - 0^2] - 0)];
y0 = N[0 + 1/2 (Sqrt[1 - x0^2] - 0)];

NestList[h, {x0, y0}, 10]

{{0.5, 0.433013}, {0.700694, 0.573237}, {0.760042, 
  0.611556}, {0.775621, 0.621377}, {0.779567, 0.623848}, {0.780556, 
  0.624467}, {0.780804, 0.624622}, {0.780865, 0.624661}, {0.780881, 
  0.62467}, {0.780885, 0.624673}, {0.780886, 0.624673}}

You are right indeed, nicely spotted :) – C. E. Oct 12 '14 at 21:23 — C. E., Oct 12 '14 at 21:23

bill s · Answer 2 · 2014-10-13T03:28:30.290

6

In an earlier edit, I had misread one of the subscripts in the y equation (thanks to Stelios for pointing this out). Here is the corrected version:

x[n_] := x[n] = x[n - 1] + 1/2 (Sqrt[1 - y[n - 1]^2] - x[n - 1]);
y[n_] := y[n] = y[n - 1] + 1/2 (Sqrt[1 - x[n]^2] - y[n - 1]);
x[0] = 0.5;
y[0] =  1/2 Sqrt[1 - x[0]^2];

x[10]

To get many values:

{x[#], y[#]} & /@ Range[0,10]

edited Oct 13 '14 at 03:28

answered Oct 12 '14 at 20:13

bill s

68,936
4
101
191

great - thank you! :) – martin Oct 12 '14 at 20:51

C. E. · Answer 3 · 2014-10-12T21:23:13.800

5

RecurrenceTable:

RecurrenceTable[{
   x[n + 1] == x[n] + (1/2) (Sqrt[1 - y[n]^2] - x[n]),
   y[n + 1] == y[n] + (1/2) (Sqrt[1 - x[n + 1]^2] - y[n]),
   x[0] == 0, y[0] == 0}, {x, y}, {n, 1, 5}] // N

{{0.5, 0.433013}, {0.700694, 0.573237}, {0.760042, 0.611556}, {0.775621, 0.621377}, {0.779567, 0.623848}}

Credit goes to Stelios for spotting a mistake in the original answer :)

edited Oct 12 '14 at 21:23

answered Oct 12 '14 at 20:13

C. E.

70,533
6
140
264

ubpdqn · Answer 4 · 2014-10-13T06:20:09.653

Using:

f[x_, y_] := x + 0.5 (Sqrt[1 - y^2] - x)

Initial condition {0,0} first 10:

NestList[Apply[Function[{x, y}, {f[x, y], f[y, f[x, y]]}], #] &, {0, 
  0}, 10]

yields:

{{0, 0}, {0.5, 0.433013}, {0.700694, 0.573237}, {0.760042, 
  0.611556}, {0.775621, 0.621377}, {0.779567, 0.623848}, {0.780556, 
  0.624467}, {0.780804, 0.624622}, {0.780865, 0.624661}, {0.780881, 
  0.62467}, {0.780885, 0.624673}}

Note fixed points on $y=\sqrt{1-x^2}$:

Manipulate[
 Show[ListPlot[
   NestList[
    Apply[Function[{x, y}, {f[x, y], f[y, f[x, y]]}], #] &, {a[[1]], 
     a[[2]]}, 10]], Plot[Sqrt[1 - x^2], {x, 0, 1}], 
  PlotRange -> Table[{0, 1}, {2}], Frame -> True, 
  FrameLabel -> {"x", "y"}, BaseStyle -> 16, 
  AxesOrigin -> {0, 0}], {a, {0, 0}, {1, 1}}]

enter image description here

I'm very happy to know that our idea is a bit same:-) – xyz Oct 13 '14 at 05:27 — xyz, Oct 13 '14 at 05:27

score 2 · Answer 5 · answered Oct 13 '14 at 05:17

Firstly,I simplify your formular:

$$x_{n}=\frac{1}{2}\left(x_{n-1}+\sqrt{1-y_{n-1}\ ^{2}}\right)\\ y_{n}=\frac{1}{2}\left(y_{n-1}+\sqrt{1-x_{n}\ ^{2}}\right)$$

Seeing the sequences as below:

$$x_1,y_1,x_2,y_2,x_3,y_3\ldots\\ $$ I define a function:$f(x,y)=1/2(x+\sqrt{1-y^2})$ $$ x_2=f(x_1,y_1)\\ y_2=f(y_1,x_2)\\ x_3=f(x_2,y_2)\ldots $$ So considering the underlying permutation :

$$(x_1,y_1),(y_1,x_2),(x_2,y_2),(y_2,x_3) \\ \ldots$$

Solutions

$x_0=1/2,y_0=\sqrt{3}/4$

To achieve:$x_0,y_0,x_1,y_1,\dots x_{12},y_{12}$

 f[x_, y_] := 1/2 (x + Sqrt[1 - y^2]);
 xyList=
   DeleteDuplicates@
    Flatten@NestList[{#[[2]], f[Sequence @@ ##]} &, {1/2, Sqrt[3]/4}, 10] // N

 {0.5, 0.433013, 0.700694, 0.573237, 0.760042, 0.611556, 0.775621, 0.621377, 
    0.779567, 0.623848, 0.780556, 0.624467}

Lastly

 xlst=xyList[[Range[1, 12, 2]]]

{0.5, 0.700694, 0.760042, 0.775621, 0.779567, 0.780556}

 ylst=xyList[[Range[2, 12, 2]]]

{0.433013, 0.573237, 0.611556, 0.621377, 0.623848, 0.624467}

Sequence generation

5 Answers5

Solutions

Linked