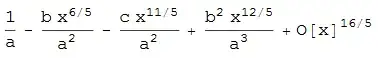Consider the following series expression:
Series[1/(a+b x^(1/3)+c x^(4/3)),{x,0,1}]
The result comes out appropriately:
1/a - b x^(1/3)/a^2 +b^2 x^(2/3)/a^3 - b^(3) x/a^4 + O[x]^(5/3)
In comparison with this, now consider the following series expansion:
Series[1/(a+b x^(Zeta[3])+c x^(1+Zeta[3])),{x,0,1}]
Here the function breaks down and gives back:
1/(a+b x^(Zeta[3])+c x^(1+Zeta[3]))
I wonder why the expansion works in the case of 1/3 but does not work for Zeta[3]? Is there a convenient way to obtain the expansion for the second case above? As always, the examples are oversimplified, so that the expansion is actually needed for expressions that are a lot bigger and unwieldy. Thanks for any suggestion!