5

Solving general differential equations in Mathematica usually leads to somewhat unsightly results.

As an example, consider the solution of the driven, damped harmonic oscillator:

eqn = x''[t] + β x'[t] +  ω0^2 x[t] == f0/m Exp[I ωd t];
s = DSolve[eqn, x[t], t]

Unsightly long result

Using FullSimplify helps to reduce this mess, but the result is still far away from something an engineer or physicist would recognize at first glance:

Simplify[s]

Weirdly simplified result

How can you transform such solutions into something nicer?

Martin J.H.
  • 753
  • 3
  • 15

2 Answers2

6

Referring to your own answer there is a much simpler form that you may use, recalling:

Collect[expr, var, h] applies h to the expression that forms the coefficient of each term obtained.

sol = x[t] /. s[[1]];

Collect[sol, _C, Simplify]

(E^(I t ωd) f0)/(m ω0^2 + I m β ωd - m ωd^2) + 
 E^(-(1/2) t (β + Sqrt[β^2 - 4 ω0^2])) C[1] + 
 E^(1/2 t (-β + Sqrt[β^2 - 4 ω0^2])) C[2]

Martin commented:

It's unfortunate that FullSimplify doesn't do this step on its own. The leaf-count is actually lower after collecting on the C[i].

One can add manipulations using TransformationFunctions therefore:

collectC[x_] := Collect[x, _C, Simplify]
SetOptions[FullSimplify, TransformationFunctions -> {Automatic, collectC}];

FullSimplify[sol]

(E^(I t ωd) f0)/(m ω0^2 + I m β ωd - m ωd^2) + 
 E^(-(1/2) t (β + Sqrt[β^2 - 4 ω0^2])) C[1] + 
 E^(1/2 t (-β + Sqrt[β^2 - 4 ω0^2])) C[2]
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • 4
    This is a nice and general method for linear differential equations because the C[i] will always be multiplicative in front of the homogeneous solutions, so collecting them is the natural choice (+1). – Jens Oct 15 '14 at 21:25
  • It's unfortunate that FullSimplify doesn't do this step on its own. The leaf-count is actually lower after collecting on the C[i]. – Martin J.H. Oct 16 '14 at 08:11
  • 1
    The result of collecting over m is smaller, but not very systematic because m is a variable that could easily be eliminated from the entire problem. A more systematic way of getting that same result seems to be Simplify /@ Apart@Simplify[sol]. Here I use the fact that Map can also work on expressions that don't have head List - which is also something the OP could have used to avoid converting to List initially. But I think what the physicist expects is really the result of collecting over _C... – Jens Oct 16 '14 at 17:55
  • @Jens Points taken. – Mr.Wizard Oct 16 '14 at 18:00
  • @Jens I updated my answer to work on _C but I did not introduce Apart. Do you feel like posting that yourself? – Mr.Wizard Oct 16 '14 at 18:04
  • I really think the _C approach is unbeatable, so this should be the accepted answer. So I'll just leave it up to you if you want to mention Apart. – Jens Oct 16 '14 at 18:09
3

One way to tackle the problem is to recognize that the solution is one giant sum with three terms.

You can then convert this sum to a list, simplify the terms individually, and sum all elements of the list back together.

sol = x[t] /. s[[1]];
Total[ FullSimplify[ Apply[ List , sol  ] ] ]

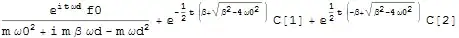
Nicer solution

But this "hack" is somewhat unelegant, because it might fail if the inhomogeneous solution is a sum in it's own.

A more robust solution is to Simplify first, then Collect all terms that contain a C[ ]-factor, and finally simplifying the individual terms in that sum:

sol = x[t] /. s[[1]];
Total [Simplify[Apply[List, Collect[ Simplify[ sol ], _C  ] ] ] ]

It's a bit hard to see what is going in that verbose form, so here is the same code in postfix notation (think "Unix pipes"):

sol = x[t] /. s[[1]];
sol // Simplify // Collect[#, _C]&   // Apply[List, #]&   // Simplify // Total

The output of all these commands is equivalent.

Addendum: I did another FullSimplify of the last result and noticed that it stayed the same (instead of reverting to the original). And indeed, checking the complexity of the expressions revealed 121 for the original "FullSimplified"-version, and 90 for the "Collected" version.

I suspect that FullSimplify somehow misses this simplification. Hopefully it will come in future Mathematica versions.

Community
  • 1
Martin J.H.
  • 753
  • 3
  • 15
  • 1
    For a very simple form, set the arbitrary constants to zero: s[[1]] /. {C[1] -> 0, C[2] -> 0} // Simplify – Bob Hanlon Oct 15 '14 at 17:13
  • 2
    It's a valid trick, but you have to be careful that you don't lose information that you care about: In the harmonic oscillator example, setting the Cs to 0 gets rid of the transients and leaves you with the steady state solution. – Martin J.H. Oct 15 '14 at 17:16
  • 1
    Another way to write your last line of code, assuming M10 operator forms: Simplify[sol] ~Collect~ C[_] // Apply[List] // Simplify // Total – Mr.Wizard Oct 15 '14 at 19:32