I noticed something weird with MatrixPlot's PlotLegends -> Automatic behavior- here's a minimal example:
MatrixPlot[Table[Exp[-((i - 25)^2 + (j - 25)^2)], {i, 50}, {j, 50}],
PlotLegends -> Automatic, ColorFunction -> "ThermometerColors"]
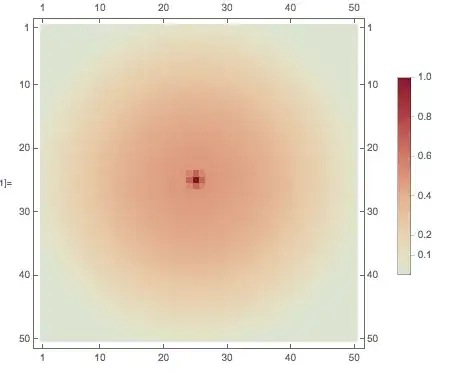
According to the plot legend, there are points with amplitude of roughly 1/2 at coordinates {25, 40}. However, at that point, the value of the matrix is 1/E^225, which means the color scheme is wrong by about one hundred orders of magnitude (!).
This has to be a bug, right? Or is this an oversight of the fact that MatrixPlot seems to use a logarithmic-like color scheme?


ArrayPlot? – Oct 17 '14 at 03:10MatrixPlot. – DumpsterDoofus Oct 17 '14 at 12:51