Using ComponentMeasurements twice, on the original matrix m and on Transpose/@m we can get all Neighbors:
mat = RandomInteger[{0, 1}, {3, 3, 3}];
m = Module[{i = 1}, mat /. 1 :> i++];
v = ComponentMeasurements[m, "Label"][[All, 1]]
{1,2,3,4,5,6,7,8,9,10,11,12,13,14}
vcoords = ComponentMeasurements[m, "Centroid"][[All, -1]]
{{0.5,2.5,2.5},{1.5,2.5,2.5},{0.5,1.5,2.5},{1.5,1.5,2.5},{0.5,0.5,2. 5},
{2.5,0.5,2.5},{2.5,2.5,1.5},{0.5,1.5,1.5},{0.5,0.5,1.5},{1.5,0.5,1. 5},
{1.5,2.5,0.5},{2.5,2.5,0.5},{2.5,1.5,0.5},{1.5,0.5,0.5}}
linksa = List @@@ DeleteDuplicates[Sort /@ Flatten[Thread /@
ComponentMeasurements[m, "Neighbors", CornerNeighbors -> False]]]
{{1,3},{2,4},{3,5},{3,8},{5,9},{7,12},{8,9},{10,14},{12,13}}
linksb = List @@@ DeleteDuplicates[Sort /@ Flatten[Thread /@
ComponentMeasurements[Transpose /@ m, "Neighbors", CornerNeighbors -> False]]]
{{1,2},{3,4},{3,8},{5,9},{7,12},{9,10},{10,14},{11,12}}
alllinks = DeleteDuplicates[Join[linksa, linksb]]
{{1,3},{2,4},{3,5},{3,8},{5,9},{7,12},{8,9},{10,14},{12,13},{1,2},{3,4},{9,10},{11,12}}
Graphics3D[GraphicsComplex[vcoords, {PointSize[Large], Red,
Sphere[#, .1] & /@ v, Thick, Blue, Line[alllinks]}]]
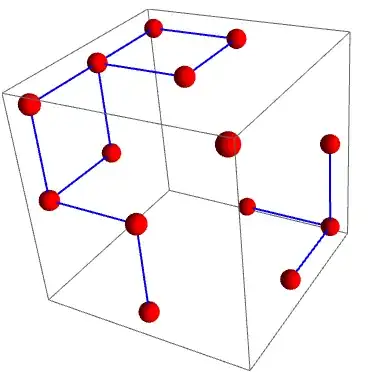
Update: a larger input matrix
mat = RandomInteger[{0, 1}, {10, 10, 10}];
(* ... same calculations for v, vcoords and alllinks as above *)
Graphics3D[GraphicsComplex[vcoords, {PointSize[Large],
Red, Sphere[#, .15] & /@ v, Opacity[.7], Orange, Tube[alllinks]}],
ImageSize -> 500, Background -> Black, Boxed -> False]
we get

Graphics3D[GraphicsComplex[vcoords,
{PointSize[Large], Red, Sphere[#, .15] & /@ v,
Opacity[.1], White, Cuboid[vcoords[[#]] - .5, vcoords[[#]] + .5] & /@ v,
Opacity[.9], Orange, Tube[alllinks]}],
ImageSize -> 500, Background -> Black, Boxed -> False]

Note: Had to use Graphics3D to produce the output instead of Graph3D
because somehow
Graph3D[UndirectedEdge@@@alllinks, VertexCoordinates->Thread[v->vcoords]]
gives Null on the free version of Wolfram Programming Cloud.
Update
This can be encapsulated as follows
ClearAll[arrayGraph];
arrayGraph[mat_, opts : OptionsPattern[]] :=
Module[{m = Module[{i = 1}, mat /. 1 :> i++], edges, edges2, vcs, v},
v = ComponentMeasurements[m, "Label"][[All, 1]];
vcs = ComponentMeasurements[m, "Centroid"];
edges =
UndirectedEdge @@@
DeleteDuplicates[
Sort /@ Flatten[Thread /@ ComponentMeasurements[m, "Neighbors",
FilterRules[Flatten[{opts}],
Options[ComponentMeasurements]]]]];
edges2 =
UndirectedEdge @@@
DeleteDuplicates[
Sort /@ Flatten[
Thread /@ ComponentMeasurements[Transpose /@ m, "Neighbors",
FilterRules[Flatten[{opts}],
Options[ComponentMeasurements]]]]];
edges = DeleteDuplicates[Join[edges, edges2]];
Graph3D[v, edges, VertexCoordinates -> vcs,
FilterRules[Flatten[{opts}], Options[Graph3D]]]]
which works as follows:
mat = RandomInteger[{0, 1}, {3, 3, 3}];
arrayGraph[mat, VertexSize -> .3, EdgeStyle -> Directive[Thick, Red],
Boxed -> True]
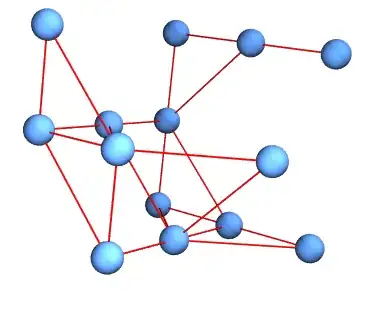
And if diagonal links are not required,
arrayGraph[mat, VertexSize -> .3, EdgeStyle -> Directive[Thick, Red],
Boxed -> True, CornerNeighbors-> False]

It works also on the skeletons
(pl = {(skl = skel[dat]) // Image3D[#, ImageSize -> 300] & //
Rasterize,Image[arrayGraph[skl // Normal, CornerNeighbors -> False],
ImageSize -> 300]}); ImageMultiply@@pl












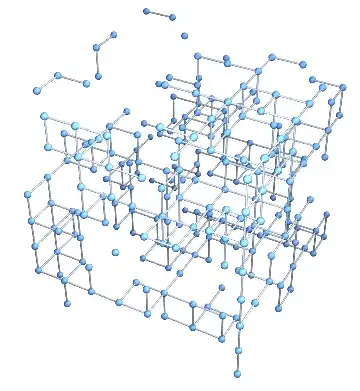



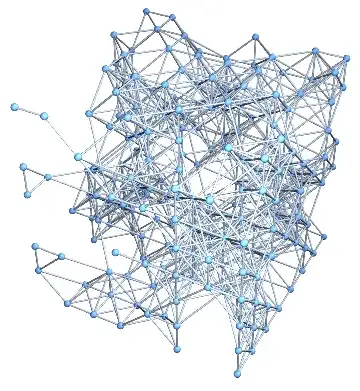
arrayGraph: add before the last lineedges2= UndirectedEdge @@@ DeleteDuplicates[Sort /@ Flatten[Thread /@ ComponentMeasurements[Transpose/@m, "Neighbors"]]];edges=DeleteDuplicates[Join[edges,edges2]];(I am using the free online version of V10, and the input matrix is too large given the limitations of the free version.) – kglr Oct 17 '14 at 20:31