0

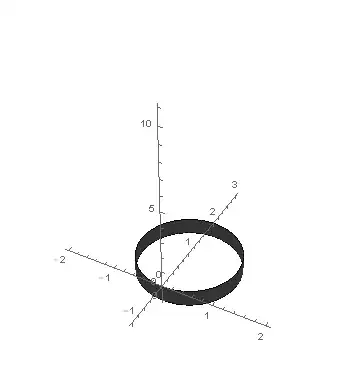
In a ContourPlot3D, I only want to part of the plot. Such as the part of a cylinder that lies beneath a plane. 

ContourPlot3D[{x^2 + (y - 1)^2 == 1, z - t y == 0}, {x, -2, 2}, {y, -1, 3}, {z, -1, 11}, 
 Boxed -> False, 
 AxesOrigin -> {0, 0, 0}]
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
xinfaxian
  • 1

2 Answers2

2
Manipulate[ContourPlot3D[
  x^2 + (y - 1)^2 == 1,
  {x, -2, 2}, {y, -1, 3}, {z, -1, 11},
  ContourStyle -> Opacity[0.5],
  Mesh -> False,
  RegionFunction -> Function[{x, y, z}, z - t y < 0],
  Boxed -> False, AxesOrigin -> {0, 0, 0}],
 {{t, 2}, 0, 5}]

Blockquote

or this is Simon Woods 's answered code

contourRegionPlot3D[
  region_, {x_, x0_, x1_}, {y_, y0_, y1_}, {z_, z0_, z1_}, 
  opts : OptionsPattern[]] := 
 Module[{reg, preds}, 
  reg = LogicalExpand[
    region && x0 <= x <= x1 && y0 <= y <= y1 && z0 <= z <= z1];
  preds = 
   Union@Cases[reg, _Greater | _GreaterEqual | _Less | _LessEqual, -1];
  Show@Table[
    ContourPlot3D[Evaluate[Equal @@ p],
     {x, x0, x1}, {y, y0, y1}, {z, z0, z1}, 
     RegionFunction -> 
      Function @@ {{x, y, z}, Refine[reg, p] && Refine[! reg, ! p]}, 
     opts], {p, preds}]
  ]

Manipulate[contourRegionPlot3D[
  x^2 + (y - 1)^2 < 1 && z - t y < 0,
  {x, -2, 2}, {y, -1, 3}, {z, -1, 11},
  Boxed -> False, AxesOrigin -> {0, 0, 0}],
 {{t, 2}, 0, 5}]
Community
  • 1
Junho Lee
  • 5,155
  • 1
  • 15
  • 33
0

Assuming x-y plane,:

ContourPlot3D[{x^2 + (y - 1)^2 == 1, z - t y == 0}, {x, -2, 2}, {y, -1, 3}, {z, -1, 11}, 
 Boxed -> False, 
 AxesOrigin -> {0, 0, 0}, 
 RegionFunction -> Function[{x, y, z}, z < 0]]

enter image description here

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
ubpdqn
  • 60,617
  • 3
  • 59
  • 148