10

I have list of pure functions (All functions are InterpolatingFunction) i.e 

{{a, b}, {c, d}, {e, f}, ...}

and I would like to end up with 

{ (a[#]/b[#])&, (c[#]/d[#])&,(e[#]/f[#])&,...}

the closest I have got is to do

(Divide @@ Through[#[x]]) & /@ {{a, b}, {c, d}, {e, f}}

{a[x]/b[x], c[x]/d[x], e[x]/f[x]}

but these are not pure functions.

rhermans
  • 36,518
  • 4
  • 57
  • 149

3 Answers3

12

This perhaps:

Function[{a, b}, a[#]/b[#] &] @@@ {{a, b}, {c, d}, {e, f}}
(* Out: {a[#1]/b[#1] &, c[#1]/d[#1] &, e[#1]/f[#1] &} *)

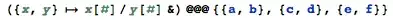
Mr.Wizard's way of writing it (see comment) looks like this in the frontend:

frontend

C. E.
  • 70,533
  • 6
  • 140
  • 264
  • 6
    Can also be written: ({x, y} \[Function] x[#]/y[#] &) @@@ {{a, b}, {c, d}, {e, f}} – Mr.Wizard Oct 21 '14 at 17:23
  • 1
    @Mr.Wizard Thanks, I hadn't seen \[Function] before! I added an image to the answer so everyone can see how it looks there. – C. E. Oct 21 '14 at 17:34
7

You can almost always turn to replacement patterns when you need to transform expressions:

Cases[
  {{a, b}, {c, d}, {e, f}},
  {x_, y_} :> (x[#]/y[#] &)
]

{a[#1]/b[#1] &, c[#1]/d[#1] &, e[#1]/f[#1] &}

Cases defaults to levelspec {1} so this is safer than using /..

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
4

Also:

With[{a = #1, b = #2}, a[#]/b[#] &] & @@@ {{a, b}, {c, d}, {e, f}}

or

x[#]/y[#] & /. {x -> #1, y -> #2} & @@@ {{a, b}, {c, d}, {e, f}}

(* {a[#1]/b[#1] &, c[#1]/d[#1] &, e[#1]/f[#1] &} *)
kglr
  • 394,356
  • 18
  • 477
  • 896