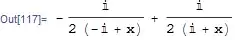Partial fraction decomposition of $1/(e^x-1)$

Question

This link has discussion on finding partial fraction decomposition of $1/(e^x-1)$, so I experimented with Mathematica to see if M can do it, but looks like not. Similar is the case with one more CAS I tried.

I can clearly see that its not working with M but question is why ?

What I think is that probably CAS gives algebraically closed solutions without extending domain hence it returns Apart[1/(x^2+1)] without success though it has roots in complex numbers(but its just a thought).

Also Apart[1/(a*x^2-1)] is not evaluated. Looks like symbolic computation on Apart is not supported or may be no such algorithm exists. Don't know !!

Can someone suggest why complex roots are not considered part of decomposition on CASes ?

Quite frankly, as a user of Mathematica, I would expect the CAS to return results based on choice whether its algebraically closed or complex roots.

@AlexeiBoulbitch Computer Algebra Systems ? E.g. Ginac++, FORM, Fermat, Mathematica, etc... Factoring, especially in denominators, tends to be their most frustrating point. — lalmei, Oct 22 '14 at 08:03
How to do partial fraction of 1/{(x^m)*((p-x^(n-1))^((n-m)/(n-1)))}? Is it possible to factorize it in Mathematica? — Sumeeta, May 18 '17 at 05:20

score 7 · Answer 1 · answered Oct 22 '14 at 15:29

7

That is not, properly speaking, a partial fraction decomposition. Those are finite and involve polynomial denominators. What you showed is a form of series representation. That can be done in Mathematica using SeriesCoefficient.

In[102]:= SeriesCoefficient[1/(Exp[x] - 1), {x, 0, n}]

(* Out[102]= Piecewise[{{BernoulliB[1 + n]/(1 + n)!, n >= -1}}, 0] *)

answered Oct 22 '14 at 15:29

Daniel Lichtblau

58,970
2
101
199

Its possible that you are correct because it doesn't look like decomposition, but there must be some partial fraction decomposition for 1/(e^x-1). I couldn't find details on this particular function. Thanks for responding though. – Pankaj Sejwal Oct 24 '14 at 08:16
Recently I read more in detail on pfd and I found that it is indeed a pfd representation.Check this link, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.49.3091 – Pankaj Sejwal Oct 26 '14 at 06:18
(1) You are correct that series coefficnets do not capture what you want, and... (2) It might be the case that there are extensions of pfd to meromorphic but not rational functions (that is, not polynomial quotients, but... (3) That cited article does not handle such functions. It is strictly for rational functions. – Daniel Lichtblau Oct 26 '14 at 19:22

score 5 · Accepted Answer · answered Oct 22 '14 at 07:35

5

Apart only factorizes the denominator in simple cases. Otherwise it needs some help:

Apart[1/Factor[(x^2 + 1), Extension -> I]]

(* -(I/(2 (-I + x))) + I/(2 (I + x)) *)

Apart[1/Factor[x^2 + 2, Extension -> {I, Sqrt[2]}]]

(* 1/(2 Sqrt[2] (Sqrt[2] - I x)) + 1/(2 Sqrt[2] (Sqrt[2] + I x)) *)

answered Oct 22 '14 at 07:35

Fred Simons

10,181
18
49

hm..I think it should be built in Apart, thanks though. – Pankaj Sejwal Oct 22 '14 at 13:45

score 4 · Answer 3 · edited Apr 13 '17 at 12:55

4

I'll use the function from Factoring polynomials to factors involving complex coefficients by Daniel Lichtblau which can also factor -1 + a x^2

factorCompletely[poly_, x_] := Module[{solns, lcoeff}, 
   solns = Solve[poly == 0, x, Cubics -> False, Quartics -> False];
   lcoeff = Coefficient[poly, x^Exponent[poly, x]];
   lcoeff*(Times @@ (x - (x /. solns)))];

Now

Apart[1/factorCompletely[-1 + a x^2, x]]

Mathematica graphics

Apart[1/factorCompletely[ x^2 + 1, x]]

Mathematica graphics

edited Apr 13 '17 at 12:55

Community

1

answered Oct 22 '14 at 08:00

Nasser

143,286
11
154
359

:thanks for bringing this link up Nasser. Its helpful. – Pankaj Sejwal Oct 22 '14 at 13:46

Partial fraction decomposition of $1/(e^x-1)$

3 Answers3