How do I solve a profile interval (statistics)

Question

I want to calculate a 95% profile interval for f0. Do worry too much if you do not understand what it is. I will illustrate with a simple example.

mylik[f0_,p_]:=Module[
    {ans},
    ans = 
    - Log[2] 
    - Log[120] 
    - Log[6227020800] 
    - Log[1124000727777607680000] 
    - Log[15511210043330985984000000] 
    + f0 Log[(1 - p)^6] 
    + 25 Log[6 (1 - p)^5 p] 
    + 22 Log[15 (1 - p)^4 p^2] 
    + 13 Log[20 (1 - p)^3 p^3] 
    + 5 Log[15 (1 - p)^2 p^4] 
    + Log[6 (1 - p) p^5] 
    + 2 Log[p^6] 
    - LogGamma[1 + f0] 
    + LogGamma[69 + f0]
];
{maxlog, mles} = NMaximize[{mylik[f0, p], f0 > 0, 0 < p < 1}, {f0, p}];
proflikfun[f0_] := Module[
    {ans, p},

    ans = NMaximize[{mylik[f0, p], 0 < p < 1}, p];
    ans = ans[[1]];
    ans = ans + Quantile[ChiSquareDistribution[1], 0.95]/2 - maxlog;
    ans
];

Now to plot the function. Because I know the answer, so I will plot the range

Plot[proflikfun[f0], {f0, 0, 20}];

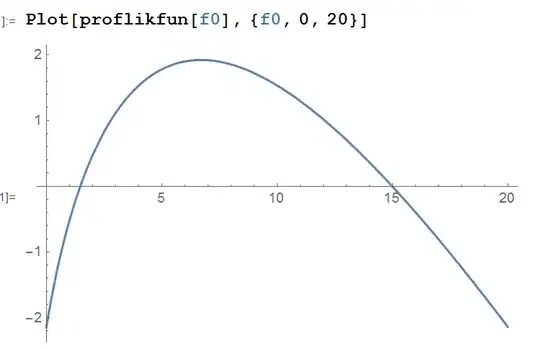enter image description here Now, how do I solve this function at 0?

I tried things like

FindRoot[proflikfun[f0] == 0, {f0, 0}]
NSolve[proflikfun[f0] == 0, {f0, 0}]

Thanks!

score 3 · Accepted Answer · edited Apr 13 '17 at 12:55

Many of the numerical functions require the function that is passed as an argument be defined for numerical arguments to that function. This is explained as one of the pitfalls here: link to SE frequent pitfalls

Your code will work as is if you use a pattern restriction ?NumericQ in your function definition:

Clear[profikfun];

proflikfun[f0_?NumericQ] := 
Module[{ans, p}, ans = NMaximize[{mylik[f0, p], 0 < p < 1}, p];
   ans = ans[[1]];
   ans = ans + Quantile[ChiSquareDistribution[1], 0.95]/2 - maxlog;
   ans];

Now you have:

FindRoot[proflikfun[f0] == 0, {f0, 0}] (*gives {f0 -> 1.47209}*)

FindRoot[proflikfun[f0] == 0, {f0, 15}] (*gives {f0 -> 14.9902}*)

How do I solve a profile interval (statistics)

1 Answers1