I have the following problem, and even though I've tried Fold & Inner, Sow & Reap, et al. I can't figure out the clean way to do this.
Here's the problem. I have a list that starts as {a,b}. I want to apply the functions f[u,v] and g[x,y,z] a fixed number of times to this list. The diagram below shows one iteration of what I want to do.

The next iteration would use this new list {A,B,b} as its input, as follows:
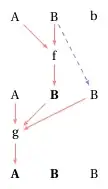
So after doing this a set number of times, I'd like the "result" to be the first two columns of these computations. That is, if I did it two times (as above), I would be left with {{a,A,A},{b,B,B}}.
I can do this with a for loop of course, but I really believe there is a more "functional programmy" approach. I know this isn't strictly about Mathematica, but it's the language I'm most comfortable with and it's related to a project I'm working on.
Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign!
– Dr. belisarius Oct 23 '14 at 17:09