Problem in finding the numerical maximum

Question

I need to find the numerical maxima of the function

$$i(s)=\bigg[ \frac{\sin{50\pi (\cos s+1)}}{\sin{10\pi (\cos s+1)}} \bigg] ^2$$

Or in the mathematica input form:

i[s_] := (Sin[50 \[Pi] (Cos[s] + 1)]/Sin[10 \[Pi] (Cos[s] + 1)])^2

Whose plot looks like this:

But Mathematica cannot find its maxima. I've tried

NMaximize[i[s], s]

Which gives a single local maximum (the help file said that this could happen for some nonlinear functions).

Table[FindMaximum[i[s],{s,x Degree}],{x,0,90}]

Returned some (not all) of the peaks, but mostly random points that are not even local maxima.

NSolve[i'[s]==0,s]

Returned some (still, not all) of the local maxima, but all the shark peaks were omitted.

So how can I get all the peaks with Mathematica? Notice that the peak occurs for every four local maxima. Thanks!

Answer 1

f = (Sin[50 Pi (Cos[#] + 1)]/Sin[10 Pi (Cos[#] + 1)])^2 &;

Plot[f[s], {s, 0, 1},
 ImageSize -> 600,
 PlotTheme -> "Detailed",
 Mesh -> {{0}},
 MeshFunctions -> {ConditionalExpression[f'[#], f''[#] < 0 && f[#] > 0] &},
 MeshStyle -> {PointSize[Large], Red}]

table = Table[f[s], {s, 0., 1, 0.0001}];

peaks = FindPeaks[table, 1];

ygrid = Round[Map[Last, peaks], 0.0001] // Union

{1., 1.5625, 25.}

ListPlot[{table, peaks},
 ImageSize -> 600,
 Filling -> {2 -> -1},
 FillingStyle -> Directive[Green, Thick],
 FrameTicks -> {{{0, 0}, {5000, 0.5}, {10000, 1}}, Automatic},
 GridLines -> {{0, 5000, 10000}, ygrid},
 Joined -> {True, False},
 PlotStyle -> {Automatic, {Red, PointSize[0.01]}},
 PlotTheme -> "Detailed"]

Answer 2

Update: The problem with NSolve is addressed in Issue with NSolve

The problem with obtaining the large peaks is that they occur where the denominator is zero. The function turns out to have a finite limit at those places, so the discontinuity is removable. Since removing it is desired, I would recommend setting the problem up, so that there is no discontinuity. TrigExpand can help.

expr = (Sin[50 π (Cos[s] + 1)]/Sin[10 π (Cos[s] + 1)])^2;
i = expr // TrigExpand // Simplify
(* (1 + 2 Cos[20 π Cos[s]] + 2 Cos[40 π Cos[s]])^2 *)

One could carry this further, if desired, to write the problem as a polynomial in Cos[20 π Cos[s]] via the double-angle formula. Mathematica sometimes figures out for itself how to do it. The reason is that polynomials are easier to deal with.

Solution 1

I suppose if one had the local maxima over a period, then in a sense one knows all the local maxima. It's perhaps not so clear that the period is π instead of 2 π.

i - (i /. s -> s + Pi) // Simplify
(* 0 *)

The easiest and possibly fastest way to get the maxima numerically is via NDSolve and WhenEvent. We start the integration a little before zero so that WhenEvent can capture the maximum at the origin.

{sol1} = N@
   Last@Reap[
     NDSolve[{f'[s] == D[i, s], f[-0.01] == (i /. s -> -0.01), 
       WhenEvent[f'[s] < 0, Sow[s]]}, f, {s, -0.01, Pi - 0.0001}]];

Plot[i, {s, -0.01, Pi},
 GridLines -> {sol1, None}, 
 GridLinesStyle -> Directive[Thin, Red], AspectRatio -> 1/10, 
 Axes -> False, Frame -> True]

Solution 2

Solve (or Reduce) of course can solve the problem exactly, although a little slowly, as others have shown. Here is my approach. It returns roots with multiplicity, so I delete the duplicates.

sol2 = DeleteDuplicates[s /. Solve[D[i, s] == 0 && i > 0 && 0 <= s < Pi, s]]

Solution 3

One can also use NSolve instead of Solve as follows:

sol3 = s /. NSolve[D[i, s] == 0 && i > 0 && 0 <= s < Pi, s]

It will be fairly fast and highly accurate.

Warning (updated): If I extend the domain to 0 <= s < 2 Pi, NSolve omits the solution at Pi. At explanation can be found in Artes' answer which is linked above. The way to get all the solution is to explicitly specify the domain Complexes:

sol3b = s /. NSolve[D[i, s] == 0 && i > 0 && 0 <= s <= 2 Pi, s, Complexes]

However, this way takes several seconds, just about as long as Solve (which gives exact results). A faster way to use NSolve to get all the solutions is to solve each factor separately:

sol3c = s /. NSolve[Power @@ ## == 0 && i > 0 && 0 <= s <= 2 Pi, s] & /@ 
   FactorList[D[i, s]] // DeleteDuplicates

For this problem NSolve would be my choice were it not for this difficulty; if highly accurate solutions are desired, then I would recommend one of these two updated methods, sol3b or sol3c. A further consideration is that NSolve is limited in the types of equations it can handle. The NDSolve approach in solution 1 works more generally. And I like NDSolve. These were my considerations behind the claim above that it's "easiest."

Answer 3

With a little help, Mathematica can give you the exact positions of all maxima. Consider

f[s_] := Sin[50 \[Pi] (Cos[s] + 1)]/Sin[10 \[Pi] (Cos[s] + 1)]

Since all minima of this function are negative and all maxima are positive, the maxima of i(s) correspond to the extreme values of f(s). Therefore, they are the zeroes of

D[f[s], s] // Simplify

(* 80 [Pi] (3 Cos[10 [Pi] Cos[s]] + 2 Cos[30 [Pi] Cos[s]]) Sin[s] Sin[10 [Pi] Cos[s]] *)

Hence the maxima of i(s) are at the positions

Solve[% == 0 && 0 <= s <= \[Pi]/2, s]

(* long output, omitted *)

Therefore, the maxima of i(s) are:

Table[{z[[1, 2]], Limit[i[s], z[[1]]]}, {z, %}]

(* long output, omitted *)

So the extrema you are looking for are

Select[%, #[[2]] == 25 &]

(* {{0, 25}, {0, 25}, {0, 25}, {[Pi]/3, 25}, {[Pi]/2, 25}, {ArcCos[1/10], 25}, {ArcCos[1/5], 25}, {ArcCos[3/10], 25}, {ArcCos[2/5], 25}, {ArcCos[3/5], 25}, {ArcCos[7/10], 25}, {ArcCos[4/5], 25}, {ArcCos[9/10], 25}} *)

Answer 4

You can employ the standard procedure to find the maxima of i[s], i.e. look for s such that i'[s]==0 and i''[s] < 0

The function in question is

i[s_] := (Sin[50 \[Pi] (Cos[s] + 1)]/Sin[10 \[Pi] (Cos[s] + 1)])^2

Plot it to get a first impression

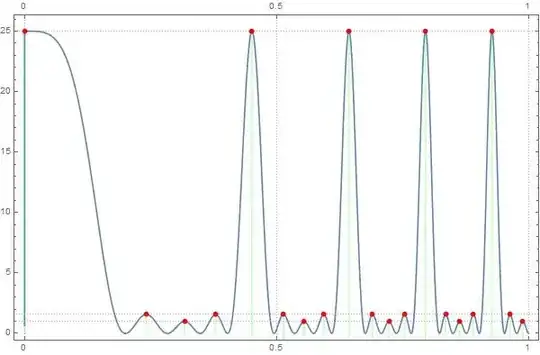
Plot[{1, i[s], i'[s], i''[s]}, {s, 0, 1}, PlotRange -> {0, 30}]

(* picture not shown here *)

Now we apply reduce to the generic conditions for the maximum

r = Reduce[(i'[s] == 0) && (i''[s] < 0)] /. C[1] -> n;
Short[r, 2]

$(n\in \text{Integers}\&\&(\langle\langle 1\rangle\rangle )\&\&\text{Sin}[s]==0)\left\|\left(n\in \text{Integers}\&\&\left(\left(\text{Sin}[s]\in \text{Reals}\&\&\text{Sin}[s]\neq 0\&\&\text{Cos}[s]==\frac{-5 \pi +n \pi +\text{ArcTan}\left[\text{Root}\left[5-22 \text{$\#$1}^2+5 \text{$\#$1}^4\&,1\right]\right]}{5 \pi }\right)\left\|\left(\text{Sin}[s]\in \text{Reals}\&\&\text{Sin}[s]\neq 0\&\&\text{Cos}[s]==\frac{1}{20} (-21+4 n)\right)\right\|(\langle\langle 1\rangle\rangle )\|(\langle\langle 1\rangle\rangle )\|(\langle\langle 1\rangle\rangle )\|\left(\text{Sin}[s]\in \text{Reals}\&\&\text{Sin}[s]\neq 0\&\&\text{Cos}[s]==\frac{-5 \pi +n \pi +\text{ArcTan}\left[\text{Root}\left[5-22 \text{$\#$1}^2+5 \text{$\#$1}^4\&,4\right]\right]}{5 \pi }\right)\right)\right)\right.$

A rather long expression results. Prominent feature is the appearance of the roots of two polynomials

Table[ArcTan[Root[1 - 10 #1^2 + 5 #1^4 &, k]], {k, 1, 4}] // N

(* Out[5]= {-0.942478, -0.314159, 0.314159, 0.942478} *)

Table[ArcTan[Root[5 - 22 #1^2 + 5 #1^4 &, k]], {k, 1, 4}] // N

(* Out[6]= {-1.11493, -0.455869, 0.455869, 1.11493} *)

As an example of how to proceed let us pick just one component

r2 = r[[2, 2, 2]]

(* Out[7]= Sin[s] \[Element] Reals && Sin[s] != 0 && Cos[s] == 1/20 (-21 + 4 n) *)

and Solve it for s, removing the trivial shift by a multiple of 2 Pi

r3 = Solve[r2, s] /. C[1] -> 0

(* Out[10]= {{s -> -ArcCos[-(21/20) + n/5]}, {s -> ArcCos[-(21/20) + n/5]}, {s -> 
   ConditionalExpression[-2 ArcTan[Sqrt[(41 - 4 n)/(-1 + 4 n)]], 
    1/4 < n < 41/4]}, {s -> 
   ConditionalExpression[2 ArcTan[Sqrt[(41 - 4 n)/(-1 + 4 n)]], 
    1/4 < n < 41/4]}} *)

In order to obtain all typical values for this component we need to go to n = 11. In fact

s1 = s /. Table[r3, {n, 0, 11}] // N;

Now we select the real roots and remove multiple roots to get

s2 = Union[Select[Round[Flatten[s1], 10^(-5)], (# \[Element] Reals) && (# > 0) &]] //
  N

(* Out[62]= {0.31756, 0.72273, 0.98843, 1.21323, 1.42023, 1.62082, 1.82348, 2.03756, \
2.27838, 2.58678} *)

These all give maximum = 1:

i[s2]

(* Out[63]= {1., 1., 1., 1., 1., 1., 1., 1., 1., 1.} *)

I leave it to the attentive and patient reader, to explore the other solutions along the same lines.

Regards, Wolfgang