Plotting two functions in one graph, with different value ranges

Question

Plot[2x, {x,0,4}];
Plot[x^2, {x,4,8}];

How do I merge these two graphs into one?

Answer 1

Here's a way that may serve you also for other purposes:

p[x_, left_, right_] := HeavisideTheta[x - left] HeavisideTheta[right - x]
Plot[{2 x p[x, 0, 4], x^2 p[x, 4, 8]}, {x, 0, 8}]

Another example:

tab = Table[x^(1/n) p[x, n, n + 1], {n, 1, 10}]; 
Plot[tab, {x, 0, 8}, PlotStyle -> Thick]

Answer 2

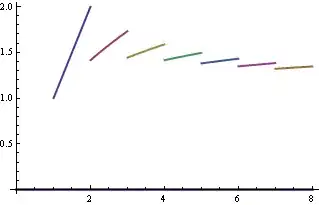
Update: Using thicker lines to make the difference between various methods visible:

Plot[{ConditionalExpression[2 x, 0 <= x < 4], ConditionalExpression[x^2, 4 < x <= 8]}, {x, 0, 8}, 
 BaseStyle -> Thickness[.02]]

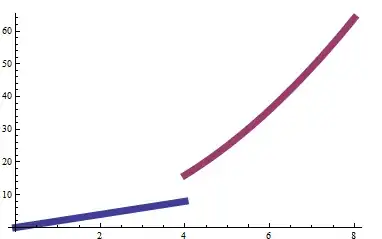
Plot[{Piecewise[{{2 x, 0<=x<4}}, Indeterminate], 
      Piecewise[{{x^2, 4<x<= 8}}, Indeterminate]}, {x, 0, 8}, BaseStyle -> Thickness[.02]]

ct = ConditionalExpression[#, #2] & @@@ Table[{x^(1/n), n < x <= n + 1}, {n, 10}];
Plot[ct, {x, 0, 8}, PlotStyle -> Thickness[.02]]

pw = Piecewise[{{#, #2}}, Indeterminate] & @@@ Table[{x^(1/n), n < x <= n + 1}, {n, 10}];
Plot[pw, {x, 0, 8}, PlotStyle -> Thickness[.02]]

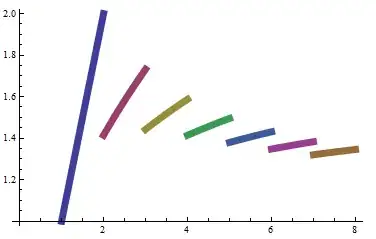
whereas,

p[x_, left_, right_] := HeavisideTheta[x - left] HeavisideTheta[right - x]
Plot[{2 x p[x, 0, 4], x^2 p[x, 4, 8]}, {x, 0, 8}, BaseStyle -> Thickness[.02]]

tab = Table[x^(1/n) p[x, n, n + 1], {n, 1, 10}];
Plot[tab, {x, 0, 8}, PlotStyle -> Thickness[.02]]

Similarly, using Boole in place of HeavisideTheta:

Plot[{2 x Boole[0 <= x <= 4], x^2 Boole[4 < x <= 8]}, {x, 0, 8}, BaseStyle -> Thickness[.02]]