Simple pattern/texture for shading chart elements

Question

If I print the following BarChart in black and white, then it is very difficult to tell which bar is "a" and which is "b".

BarChart[{{1, 2}}, ChartLegends -> {"a", "b"}]

enter image description here

Question

How can I put a simple pattern or texture (like stripes or dots) on these bars to differentiate them? I know that the solution will involve ChartElements, but I can't figure it out.

Some downvoters should ask for a mirror – Dr. belisarius Nov 01 '14 at 02:52 — Dr. belisarius, Nov 01 '14 at 02:52

score 5 · Accepted Answer · answered Nov 01 '14 at 01:56

5

BarChart[{{1, 2}}, ChartLegends -> {"a", "b"}, 
                    ChartStyle -> {GrayLevel[.1], GrayLevel[.8]}]

Mathematica graphics

answered Nov 01 '14 at 01:56

Dr. belisarius

115,881
13
203
453

That would work, but I would prefer it there were some sort of pattern as well. Can you make one have stripes or dots? – Tyson Williams Nov 01 '14 at 01:58
1

@TysonWilliams Yes, but it won't scale well when you have more bars,and this one will. – Dr. belisarius Nov 01 '14 at 01:59
Scaling is definitely needed since this BarChart is just a MWE. My actual BarChart does only have two types of bars though. – Tyson Williams Nov 01 '14 at 02:16

Alexey Popkov · Answer 2 · 2016-04-28T07:05:50.027

How can I put a simple pattern or texture (like stripes or dots) on these bars to differentiate them? I know that the solution will involve ChartElements, but I can't figure it out.

May be you need something similar to the following?

opts = Sequence[Axes -> False, PlotStyle -> None, 
   PlotRangePadding -> 0, ImagePadding -> 0];
Show[BarChart[{{3, 4}}], 
 BarChart[{{3, 4}}, 
  ChartElements -> {Plot[{ArcTan[x], ArcTan[x] + .8}, {x, -Pi/2, Pi/2}, 
                         Filling -> {1 -> {{2}, Blue}}, Evaluate@opts],
                    Plot[{-Sin[x], -Sin[x] + .8}, {x, -Pi/2, Pi/2}, 
                         Filling -> {1 -> {{2}, Red}}, Evaluate@opts]}]]

g1[{{xmin_, xmax_}, {ymin_, 
    ymax_}}, ___] := {{Hue[RandomReal[]], Point@#} & /@ 
   FindClusters[
    Transpose[{RandomReal[{xmin, xmax}, 300], 
      RandomReal[{ymin, ymax}, 300]}], 15], Black, Thin, 
  Line[{{xmin, ymin}, {xmin, ymax}, {xmax, ymax}, {xmax, ymin}}]}
g2[{{xmin_, xmax_}, {ymin_, 
    ymax_}}, ___] := {EdgeForm[None], Hue[RandomReal[]], #} & /@ 
  MeshPrimitives[
   VoronoiMesh[
    Transpose[{RandomReal[{xmin, xmax}, 300], 
      RandomReal[{ymin, ymax}, 300]}], {{xmin, xmax}, {ymin, ymax}}], 
   2]
BarChart[{{3, 4}}, ChartElementFunction -> {g1, g2}]

marble := ListCurvePathPlot[RandomReal[{0, 10}, {2000, 2}], PlotRange -> All, 
    PlotRangePadding -> 0, Axes -> False] /. l_Line :> {Hue[RandomReal[]], l};
BarChart[{1, 2, 3, 4}, ChartElements -> Table[{marble, All}, {4}]]

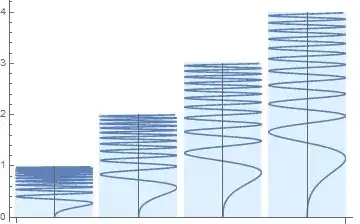
BarChart[{1, 2, 3, 4}, 
 ChartElements -> 
  ParametricPlot[{Sin[y^3], y}, {y, 0, 7}, Axes -> True, 
   Ticks -> None, Background -> LightBlue, PlotRangePadding -> 0, 
   ImagePadding -> 0]]
BarChart[{1, 2, 3, 4}, 
 ChartElements -> {{ParametricPlot[{Sin[y^3], y}, {y, 0, 4}, 
     Axes -> True, Ticks -> None, Background -> LightBlue, 
     PlotRangePadding -> 0, ImagePadding -> 0], All}}]

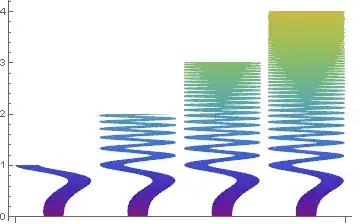
The springs with varying thickness and color (thanks to Vitaliy Kaurov!):

spring[heigh_: 5] := 
 Show[With[{amp = .1}, 
    Plot[{amp (3.5 + Sin[(Pi x)/heigh]^(1/2)) + 
       Sin[x^3], -amp (3.5 + Sin[(Pi x)/heigh]^(1/2)) + 
       Sin[x^3]}, {x, 0, heigh}, PlotPoints -> 50, 
     Filling -> {2 -> {1}}, PlotStyle -> {Gray, Gray}, 
     ColorFunction -> Function[{x, y}, Directive[ColorData["Rainbow"][x]]], 
     AspectRatio -> 4, ImageSize -> {Automatic, 500}]] /. {x_Real, y_Real} :> {y, x},
     PlotRange -> All, PlotRangePadding -> 0, Axes -> False]

BarChart[{1, 2, 3, 4}, ChartElements -> spring[10]]
BarChart[{1, 2, 3, 4}, ChartElements -> {{spring[], All}}]

pl1

pl2

score 0 · Answer 3 · answered Nov 01 '14 at 09:06

0

You can use both ChartLabels and ChartLegends for when the colors may not be easily differentiated.

BarChart[{{1, 2, 3}, {1, 3, 2}, {5, 2, 1}},
 ChartLabels -> {"a", "b", "c"},
 ChartLegends -> {"a", "b", "c"}]

enter image description here

answered Nov 01 '14 at 09:06

Bob Hanlon

157,611
7
77
198

Simple pattern/texture for shading chart elements

Question

3 Answers3