0

I want to multiply 1000by1000 matrices but MMA runs out of RAM.

LaunchKernels[]

dim = 1000;(*dimension of the matrices. There is 1000 of these 1000by1000 matrices*)

v = Developer`ToPackedArray[
Table[{
       Table[

      N@(KroneckerDelta[i, j] + Sin[i*j]) 

      , {j, 1, dim}]}
, {i, 1, dim}]];(* The matrices themselves.*)

Developer`ToPackedArray[
  ParallelSum[
              Cos[i*k]*(v[[k]]\[Transpose].v[[i]] + v[[i]]\[Transpose].v[[k]])
, {i, 1, dim}, {k, 1, dim}]];(*Multiplication part and summation*)

Here is a snapshot of task manager. I ran the code then killed the kernels:

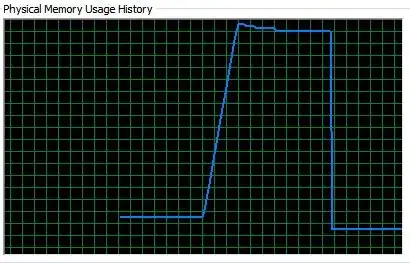
enter image description here

How can I improve this code. The problem is MMA uses a lot of RAM. I even used packed array but it didn't help. I know that in the summation part I am summing the transpose of the multiplied matrices and I could not to do the multiplication for the second term.

I edited the question to reflect the real problem better. I used $HistoryLength = 0;, it didn't help.

Edit2

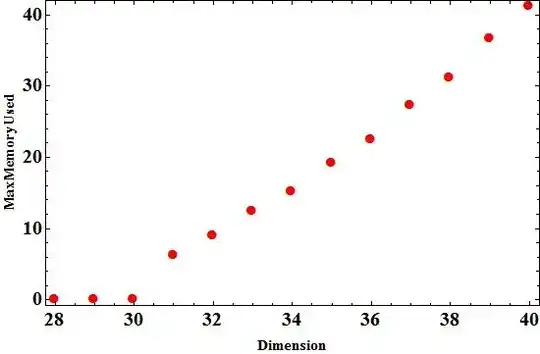
I want to see the effect of using packed arrays so I changed the dimension of the matrices and calculated the maximum used memory in the process of evaluation of those multiplications. For packed arrays I used:

v[dim_] := 
 Developer`ToPackedArray[
  Table[{Table[N@(KroneckerDelta[i, j] + Sin[i*j]), {j, 1, dim}]}, {i,
     1, dim}]];(*The matrices themselves.*)

m1 = MaxMemoryUsed[]/N[10^6]

res = Table[{MaxMemoryUsed[]/N[10^6] - m1, 
   Developer`ToPackedArray[
     Table[Cos[1.0*i*k]*(v[dim][[k]]\[Transpose].v[dim][[i]]), {i, 1, 
       dim}, {k, 1, dim}]];}, {dim, 28, 40}](* I removed the addition to the transpose  in contrast to the code provided in the above*)

axis = Table[i, {i, 28, 40}];

ListPlot[
Join[{axis}\[Transpose], {Cases[Flatten[res], _Real]}\[Transpose], 2], 
 PlotMarkers -> {\[FilledCircle], 15},
 PlotStyle -> Red, 
 Frame -> True, 
 FrameLabel -> {Style["Dimension", Bold, FontSize -> 15], Style["MaxMemoryUsed", Bold, FontSize -> 15]}, 
 FrameStyle -> Directive[Black, Bold, 20]]

Here is the result:

enter image description here

and here the result for the case I did not use packed arrays. After I got the result for packed arrays, I restart kernels.

v2[dim_] := 
  Table[{Table[N@(KroneckerDelta[i, j] + Sin[i*j]), {j, 1, dim}]}, {i,
     1, dim}];

m1 = MaxMemoryUsed[]/N[10^6]

res2 = Table[{MaxMemoryUsed[]/N[10^6] - m1, 
   Table[Cos[i*k]*(v2[dim][[k]]\[Transpose].v2[dim][[i]]), {i, 1, 
      dim}, {k, 1, dim}];}, {dim, 28, 40}]

axis = Table[i, {i, 28, 40}];

ListPlot[Join[{axis}\[Transpose], {Cases[
     Flatten[res2], _Real]}\[Transpose], 2], 
 PlotMarkers -> {\[FilledCircle], 15}, PlotStyle -> Blue, 
 Frame -> True, 
 FrameLabel -> {Style["Dimension", Bold, FontSize -> 15], 
   Style["MaxMemoryUsed", Bold, FontSize -> 15]}, 
 FrameStyle -> Directive[Black, Bold, 20]]

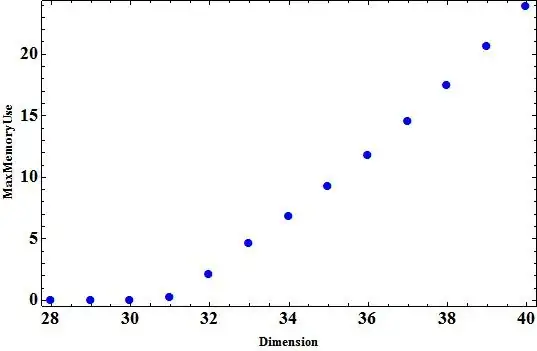
enter image description here

It seems using packed arrays is not memory efficient temporary. Can anybody reproduce these results?

MOON
  • 3,864
  • 23
  • 49
  • Would you not be better off with sparse arrays? – Yves Klett Nov 07 '14 at 12:14
  • I don't know about that. But because later in the calculations these matrices won't be sparse, it won't help me even if it help this particular situation. – MOON Nov 07 '14 at 12:16
  • Multiplying large matrices I'd use GPU support (CUDA etc.) see e.g. Would a better graphics card or more cores make Mathematica faster? – Artes Nov 07 '14 at 12:18
  • But that is not the case here. If only every millionth part will be non-zero, then SparseArray should be considered. You can work with those just like with any other matrix. – Yves Klett Nov 07 '14 at 12:18
  • @YvesKlett. I just made the example simple. If someone is interested, they can consider 1000by1000 random matrices. – MOON Nov 07 '14 at 12:23
  • before you can use parallel computing (like ParallelSum), first of all you need distribute definition of variables in parallel kernels with SetSharedVariables – molekyla777 Nov 07 '14 at 12:25
  • @Artes. I do not have GPU. I have Intel xeon CPU 3.4GHz with six cores and 24GB RAM. – MOON Nov 07 '14 at 12:26
  • My point is that the example in the question should at least reflect your real problem. Otherwise you will get solutions that are not what you are after and everyone will waste time. – Yves Klett Nov 07 '14 at 12:32
  • @molekyla777 I used SetSharedVariable[v], and v is the set of 1000 of 1000by1000 matrices. But it slows down the computation a lot. – MOON Nov 07 '14 at 12:50
  • 1
    It seems to me that t = Total[v]; u = Transpose[t].t; result = u + Transpose[u]; will give the same result in a fraction of the time. – Simon Woods Nov 07 '14 at 13:01
  • 1
    As a side note: 1) built-in matrix multiplication is already parallelized 2) CUDA acceleration for dense matrix multiplication is not very big because the speed of dense matrix multiplication depends on the size of the processor cache and CPU have a quite big cache. – ybeltukov Nov 07 '14 at 13:13
  • @SimonWoods Your solution works. However, I realized I made the example too simple. There a factor behind the summation of those matrices which prevent summation acts independently on each index. – MOON Nov 07 '14 at 13:59
  • 1
    @molekyla777 That is not correct. SetSharedvariable does not distribute definitions, it has a completely different purpose. DistributeDefinitions is used for distributing definitions but since Mathematica 8 this happens automatically when using ParallelSum. – Szabolcs Nov 07 '14 at 14:44
  • @yashar Mathematica does parallelization by launching extra kernel processes, and effectively creating a new copy of the data you're working with for each of them. If you have 4 kernels, you'll need 4 times the memory. There's a tradeoff here between being memory efficient and fast. There's also an unfortunate bug which may cause packed arrays to be temporarily unpacked after they're returned form parallel kernels. – Szabolcs Nov 07 '14 at 14:47
  • Try this instead w = First@Transpose[v]; f = Array[Cos[#1 #2] &, {dim, dim}]; u = Transpose[w].f.w; result = u + Transpose[u]; – Simon Woods Nov 07 '14 at 15:18
  • @SimonWoods Thank you. That solved my problem. However, I wish there was a solution about the fact that MMA uses RAM a lot. I ran the same code on Matlab and it won't crash because of the RAM shortage. – MOON Nov 07 '14 at 17:05
  • @SimonWoods Do you know why your solution is faster? I calculated by hand and arrived from my original multiplication to the form you suggested. The number of arithmetic operations is the same but in the form you suggested it's faster. – MOON Nov 07 '14 at 17:09
  • Yes I figured the question was more about the memory usage than the specific example, that's why I posted a comment instead of an answer. All I can really say about the speed is that I know that Dot is super-optimised for packed arrays, far far quicker than the equivalent number of arithmetic operations. I expect @ybeltukov or @Szabolcs could give a more knowledgeable explanation. – Simon Woods Nov 07 '14 at 17:33

0 Answers0