How to get Mathematica to show limit of a recurrence sequence?

Question

I want to find the limit of a such a sequence:

$f(n+1)=\sqrt{2f(n)-1}, \, f(0)=a, a>1$

How does one do this? Is it possible to have it show the solution algebraically, like it does with standard (non-recurrence) limits in WolframAlpha? (I wasn't able to do it on WolframAlpha).

score 6 · Answer 1 · edited Jun 16 '20 at 09:23

For the recursive formula

$$a_{n+1}=\sqrt{2a_{n}-1}$$

Solving $$\lim_{n\rightarrow \infty} a_n$$

It is equivalent to solve the equation $x=\sqrt{2x-1}$

$$\Rightarrow x=1$$

Update

For fixed-point theory $x=\phi(x) \quad (x>1)$

$0<|\phi'(x)|=\frac{1}{\sqrt{2x-1}}<\frac{1}{\sqrt{2\times 1-1}}=1$
$x \in [a+1,a+2] \Rightarrow \phi(x)\in [\sqrt{2a+1},\sqrt{2a+3}]\subseteq [a+1,a+2]$ where $a>1$

So for arbitary initial value $x_0 \in [a+1,a+2]$, the recursive formula $x_{k+1}=\phi(x_k) \quad (k=0,1,2 \cdots)$ is convergent.

score 4 · Answer 2 · answered Nov 08 '14 at 07:07

Just for fun you can visualize the rate of convergence for various starting position (and the monotony of approach to 1):

f[n_, p_] := Nest[Sqrt[2 # - 1] &, p, n]
Manipulate[
 Column[{DiscretePlot[f[j, p], {j, 1, n}, PlotRange -> {0, 10}, 
    GridLines -> {None, {1}}, GridLinesStyle -> Red, ImageSize -> 500],
   With[{ladder = 
      Join @@ ({#, {Last@#, Last@#}} & /@ 
         Partition[f[#, p] & /@ Range[0, n], 2, 1])},
    Plot[{Sqrt[2 x - 1], x}, {x, 0, 20}, 
     Epilog -> {Arrow[ladder], {Red, PointSize[0.02], Point[{1, 1}]}},
      ImageSize -> 500]]
   }], {n, Range[10, 100, 45]}, {p, 1.1, 20, Appearance -> "Labeled"
  }]

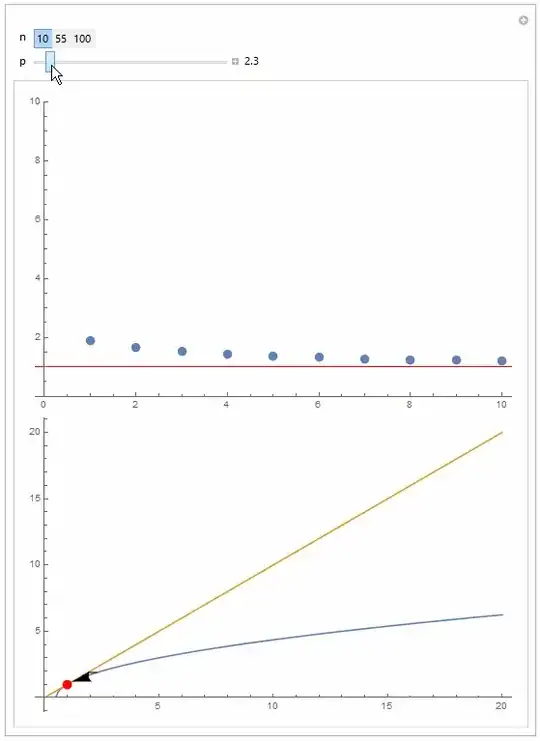
enter image description here

NestList and ListPlot could have been used instead of DiscretePlot

score 3 · Answer 3 · answered Mar 18 '19 at 03:55

As an update, I just wanted to add that in Version 11.2 and later, the limit of this sequence can be obtained using RSolveValue by giving a numerical initial value as follows.

In[1]:= RSolveValue[{f[n + 1] == Sqrt[2*f[n] - 1], f[0] == 3}, f[Infinity], n]

Out[1]= 1

Devendra Kapadia, Wolfram Research, Inc.

Bob Hanlon · Answer 4 · 2014-11-08T05:35:24.143

Clear[f];

As stated in previous answer, in the limit the equation becomes

eqn = f[n] == Sqrt[2 f[n] - 1];

Solve[eqn, f[n]][[1]]

{f[n] -> 1}

So the limit of the sequence is 1. This can also be demonstrated with FixedPoint; however, since the sequence converges very slowly it is best to start with an initial value (a) very close to 1.

FixedPoint[Sqrt[2 # - 1] &, 1.0001]

1.

EDIT: To demonstrate how slowly this converges

fpl = FixedPointList[Sqrt[2 # - 1] &, 1.0001];

Length[fpl]

76684440

 fpl[[-1]]

1.

How to get Mathematica to show limit of a recurrence sequence?

4 Answers4

Update