Is there a simple way in Mathematica to check under what conditions an expression (involving multiple variables) falls within a given range? For example, say I had a real-valued function f(x,y,z), where x,y,z are real numbers. I want to find the set S such that f(x,y,z) > 0 whenever (x,y,z) are contained in S. Is there a way to do this?
1 Answers
Tutorial The Representation of Solution Sets is a great start. Generally it depends on f(x,y,z) if you can find a solution. In many particular cases you can find reduced forms. Quoting the tutorial:
Any combination of equations or inequalities can be thought of as implicitly defining a region in some kind of space. The fundamental function of
Reduceis to turn this type of implicit description into an explicit one.
Examples of usage:
1) A multivariate polynomial inequality:
Reduce[x^2 - 3 y + z^2 > 0, {x, y, z}, Reals]
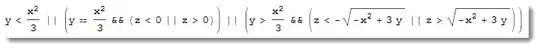
2) Systems of polynomial equations and inequalities can always be reduced:
Reduce[x^2 + y z >= 0 && x + 2 y <= 3 + 1 && y z > 7, {x, y, z}, Reals]
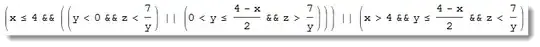
Mathematica has also related visualizations and some interesting functions, like SemialgebraicComponentInstances that "gives at least one sample point in each connected component of the semialgebraic set defined by the inequalities". This example finds at least one sample points inside a solid and visualizes it.
ineqs = x^2 + y^2 + z^2 - 7 x y z < 1 && x^2 + y^2 > 2 z^3 + 5/4 &&
x^2 + y^2 + z^2 < 3; r = 1.7;
pts = SemialgebraicComponentInstances[ineqs, {x, y, z}];
Show[{RegionPlot3D[ineqs, {x, -r, r}, {y, -r, r}, {z, -r, 1},
PlotStyle -> Directive[Yellow, Opacity[0.5]], Mesh -> None,
PlotPoints -> 35],
Graphics3D[{Red, PointSize[0.01], Point[{x, y, z} /. pts]}]},
SphericalRegion -> True]

To check points indeed belong to solid:
And @@ (ineqs /. pts)
True
- 73,078
- 9
- 204
- 355
-
For algebraics, in addition to
SemialgebraicComponentInstances[], the functionCylindricalDecomposition[]might also be of interest. – J. M.'s missing motivation Jun 08 '12 at 05:38
fand what you expect to get, since the question is too general for a constructive answer. Iffis a polynomial or a transcendental function, if you expect an exact solution, a numerical approximation or to get only some idea how that region looks like, in this case look e.g. at answers to this question : http://mathematica.stackexchange.com/questions/2897/how-to-find-regions-that-satisfy-this-inequality – Artes Jun 08 '12 at 00:35