As far as I can tell, Interpolation uses cubic spline interpolation by default - please correct me if I'm wrong.
What does it use for extrapolation outside of the range of specified x-values?
With cubic spline interpolation, the second derivative at the end points is zero, and so extrapolating along a straight line seems natural. However, that's not what happens:
![Screenshot of <code>Plot[Interpolation[{{-2, 0}, {-1,-1 }, {1, 1}, {2, 0}}][x], {x, -3, 3}]</code>](../../images/6421dd85eafa0a6ccf70e52b93c63eb9.webp)
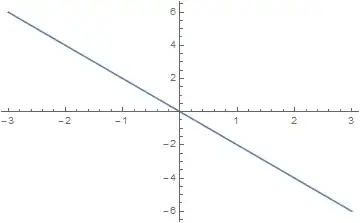
fandpwfas in my answer, check outf[x] - pwf /. {{x -> -10}, {x -> 50}}and you will see that extrapolation coincides with the interpolating formulas at the ends of the domain (which is what I would expect). – Michael E2 Nov 21 '14 at 21:57Method -> "Spline"it doesn't use natural splines. – Nov 22 '14 at 06:58