Visual representation of a Ranking over time (image provided)

Question

[Disclaimer: I initially posted this question on stackOverflow 2 months ago and think it might be better suited for this forum (link to original question)]

The graph below shows a ranking of countries at 10 different points. The cool thing with this graph is that it allows you to track changes in the ranking over time. I want to create create something similar, but I have no idea how it was created...

My guess is that it was created using some design tool like adobe indesign, but my hope is that there might be some other tools for obtaining such a graphic using Mathematica? (e.g. using Mathematica's table and network functions?)

Any ideas and/or suggestions on where to look would be much appreciated.

Country Ranking Over Time

This type of chart is used for many purposes. Here is another example of similar chart: (just for illustration purposes)

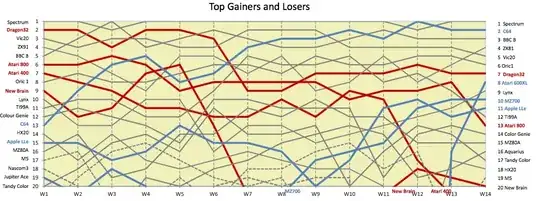
Another example

Update: @Dr.belisarius solution still stands strong as a great solution to my question from a few years ago now, but I wanted share the following:

The graph I was looking for has a name and it is a parallel coordinates plot.
For those interested, an alternative earlier Mathematica implementation of this can be found here: http://www.stats.uwo.ca/faculty/aim/2003/mviz/web/notebooks/default.htm

I'm sure people here could figure out how to make a nice looking plot... but we would need to know where to access the data from which the plot is made. — bill s, Nov 25 '14 at 21:41
Related: http://stackoverflow.com/questions/11751062/motorsport-lap-chart-revisited http://stackoverflow.com/questions/5655224/motorsport-lap-chart-using-listlineplot — Dr. belisarius, Nov 28 '14 at 12:21

score 38 · Accepted Answer · edited Apr 13 '17 at 12:56

38

Some function definitions first. AkimaInterpolation[] stolen from here:

AkimaInterpolation[data_] := Module[{dy}, dy = #2/#1 & @@@ Differences[data];
  Interpolation[Transpose[{List /@ data[[All, 1]], data[[All, -1]], 
     With[{wp = Abs[#4 - #3], wm = Abs[#2 - #1]}, 
        If[wp + wm == 0, (#2 + #3)/2, (wp #2 + wm #3)/(wp + wm)]] & @@@
      Partition[Join[{{3,-2},{2,-1}}.Take[dy,2],dy,{{-1,2},{-2,3}}.Take[dy, -2]],4,1]}], 
   InterpolationOrder -> 3, Method -> "Hermite"]]
cfun = Log@# &;

Now a simulation for your data. Please next time include a sample dataset in your question. Finding a "right" shuffle function was the most convoluted part!

c = StringInsert[#, "  ", {1, -1}] & /@ CountryData["SouthAmerica", "UNCode"];
rc = Range@Length@c;
numpoints = 8;
rn = Range@numpoints; 
vals = Most@Reverse@FoldList[
       (While[Max@Abs[#1-(tc= Permute[#1, Cycles[{RandomSample[#1, #2]}]])] > #2]; tc) &,
                             rc, rn];
xcoords = cfun /@ rn;
data = Transpose[Partition[#, 2] & /@ (Riffle[##, {1, -2, 2}] & @@@ 
                                                           Transpose[{vals, xcoords}])];

Finally the plot:

MapIndexed[(h[#2[[1]]] = AkimaInterpolation[#1]) &, data];
cd = (ColorData["Rainbow"][1 - #/Length@rc] & /@ rc);
Show[
 Plot[Evaluate[h[#][x] & /@ rc], {x, cfun@1, cfun@numpoints}, 
  PlotStyle -> ({Opacity[.6], Thickness[.01], #} & /@ cd), 
  PlotRange -> {{cfun@1, cfun@numpoints}, {-1, 16}},
  AxesOrigin -> {cfun@1, 0},
  Method -> {"FrameInFront" -> False},
  FrameTicks -> {{Transpose[{rc, c[[Last[vals]]]}], 
                  Transpose[{rc, c[[First[vals]]]}]}, {None, None}},
  Axes -> False,
  Frame -> {{True, True}, {False, False}}], 
 ListPlot[data,  PlotStyle -> ({Opacity[1], PointSize[.015], #} & /@ cd)], 
PlotRangeClipping -> False]

Mathematica graphics

edited Apr 13 '17 at 12:56

Community

1

answered Nov 26 '14 at 03:25

Dr. belisarius

115,881
13
203
453

Interesting... I have a nice application for that chart. +1 – Murta Nov 28 '14 at 00:46
Almost no difference using Interpolation[#, InterpolationOrder -> 2, Method -> "Spline"]& instead of AkimaInterpolation. – Murta Nov 28 '14 at 01:05
1

@Murta Compare the normal interpolation (order 3), at left with Akima at right. I find Akima far better for this application – Dr. belisarius Nov 28 '14 at 04:09
Ok! You are right. Curves don't dance so much with Akima (a kind of bad music interpolation). Tks – Murta Nov 28 '14 at 11:52
@Murta Yup, I tried to achieve that "flatness" with normal interpolation by varying the method and degree to no avail. – Dr. belisarius Nov 28 '14 at 12:12
data can be created using MapIndexed[{Last@#2, #1} &, Transpose@vals, {-1}]. I learned Riffle third argument from your answer. – Murta Nov 28 '14 at 22:13
Glad Akima was useful. :) Didn't Steffen work for this? Akima can still be wiggly, but the risk is not as great as with splines. – J. M.'s missing motivation May 02 '15 at 02:47
@belisarius You get one upvote and start updating your answers :D – Sektor Sep 08 '15 at 16:20
@Sektor it makes me revise old work, yes :) – Dr. belisarius Sep 08 '15 at 16:51
@belisarius Yes, I've noticed that when have upvoted other old answers of yours. – Sektor Sep 08 '15 at 16:57

Visual representation of a Ranking over time (image provided)

1 Answers1