6

Bug introduced in 8.0.4 or earlier and persisting through 12.0 or later

Check this example:

Attributes[Unevaluated]
(*{HoldAllComplete, Protected}*)
FullForm[Unevaluated[{{5 + 6}, {7 + 8}}]]
(*Unevaluated[List[List[Plus[5, 6]], List[Plus[7, 8]]]]*)

now:

TreeForm[Unevaluated[{{5 + 6}, {7 + 8}}]]

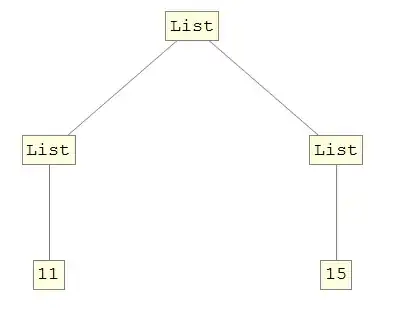
enter image description here

expr = Unevaluated[{{5 + 6}, {7 + 8}}]

(*{{11}, {15}}*)

Note here the result is like Unevaluated is not applied at all.

It looks like (according to the documentation also) that Unevaluated uses its Attributes ONLY once.

When compared with HoldComplete, which has same Attributes, the results are different and as expected.

in the case of HoldComplete:

FullForm[HoldComplete[{{5 + 6}, {7 + 8}}]]
(*HoldComplete[List[List[Plus[5, 6]], List[Plus[7, 8]]]]*)
TreeForm[HoldComplete[{{5 + 6}, {7 + 8}}]]

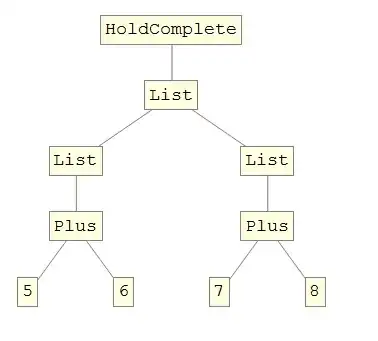
enter image description here

It is clear that the TreeForm does not represent the FullForm when using Unevaluated and works perfectly in the case of HoldComplete.

How does that happen with Unevaluated?

Alexey Popkov
  • 61,809
  • 7
  • 149
  • 368
Basheer Algohi
  • 19,917
  • 1
  • 31
  • 78
  • @kuba, you can see that the TreeFrom does not represent the FullForm. the TreeForm is like Unevaluated is not applied at all. Furthermore the result of expr = Unevaluated[{{5 + 6}, {7 + 8}}] is also like Unevaluated is not applied. I will try to edit the equation now. – Basheer Algohi Nov 26 '14 at 09:08
  • Relevant StackOverflow thread: "Why does TreeForm[Unevaluated[4^5]] evaluate the 4^5?" – Alexey Popkov Nov 28 '14 at 21:07
  • Related: 1, 2. – Alexey Popkov Nov 28 '14 at 21:12
  • I'd say Unevaluated is underdocumented. But I do not see a bug here. Internals of function implementations are allowed to strip Unevaluated and presumably TreeForm is doing just that. – Daniel Lichtblau Mar 06 '17 at 15:22
  • @DanielLichtblau "Internals of function implementations are allowed to strip Unevaluated" - Isn't this called evaluation leak? – Alexey Popkov Aug 22 '19 at 05:12
  • @DanielLichtblau There is an old discussion of this issue on SO: https://stackoverflow.com/questions/5722679/mathematica-why-does-treeformunevaluated45-evaluate-the-45#comment6551856_5723277 – Alexey Popkov Aug 22 '19 at 05:37
  • @DanielLichtblau Actually Unevaluated is sufficiently well documented for such a basic use cases: apart from ref/Unevaluated there is also tutorial/Evaluation which adds significant information. The example on ref/Unevaluated Length[Unevaluated[5 + 6 + 7 + 8]] correctly gives 4 what demonstrates the expected behavior of Unevaluated. If Length's internals would be allowed to evaluate the expression, the Unevaluated would be just pointless. – Alexey Popkov Aug 22 '19 at 06:14
  • @DanielLichtblau Hence the expected behavior is that Unevaluated should be stripped by the evaluator which must temporarily set the HoldAllComplete attribute to TreeForm. Then the unevaluated expression should be processed by TreeForm's internals without evaluating it. – Alexey Popkov Aug 22 '19 at 06:18

1 Answers1

7

What you observe is a bug (evaluation leak) inside of TreeForm. In particular, observe this:

TreeForm[Unevaluated[Print[5 + 6]]]

11
11

As you see, Print is evaluated twice inside of the TreeForm code. It is apparent bug and I suggest you to report it to technical support.

Note that in Mathematica 5.2 TreeForm doesn't have the evaluation leak:

enter image description here

There is no leak in the terminal interface in newer versions too:

enter image description here

From this comes a workaround - just wrap TreeForm with OutputForm:

TreeForm[Unevaluated[Print[5 + 6]]] // OutputForm

enter image description here

Note that this behavior is still not completely in accord with the Documentation for Unevaluated: since TreeForm doesn't have the HoldAllComplete attribute, the Unevaluated wrapper should be stripped off on the first stage of the evaluation process temporarily setting this attribute to TreeForm (refs: "Details" section on ref/Unevaluated and the fourth bullet point under the "The Standard Evaluation Sequence").

Also TreeForm displays strings without quotes by default what makes it difficult to separate them from Symbols. But on the base of this feature we can easily make the correct treeForm by converting all the Symbols and Strings into InputForm strings:

treeForm[expr_, opts___] := 
 TreeForm[Unevaluated[
    expr] /. {s : (_Symbol | _String) :> ToString[Unevaluated[s], InputForm]}, opts]

treeForm[Unevaluated[Print[5 + 6 + "string"]], ImageSize -> 300, PlotRangePadding -> .4]

screenshot

But it still requires additional work to make it working correctly with Image and probably some other atomic objects.

Alexey Popkov
  • 61,809
  • 7
  • 149
  • 368
  • Alexey Pokov, sorry for late reply. I think the problem is with Unevaluated not TreeForm. check expr = Unevaluated[{{5 + 6}, {7 + 8}}] you will see that this will evaluate Unevaluated argument. – Basheer Algohi Dec 02 '14 at 18:11
  • The expected behavior of TreeForm should be as in this example: treeForm@Unevaluated[{{5 + 6}, {7 + 8}}] (it is the documented behavior). Your example is principally different and actually is a special case (undocumented). – Alexey Popkov Dec 02 '14 at 19:03
  • I don't think it is a special case. Unevaluated evaluate its argument whenever some other operation are carried out. for example: Unevaluated[{{5 + 6}, {7 + 8}}]*1 or Unevaluated[{{5 + 6}, {7 + 8}}] + 0. Still something not clear about the behavior of Unevaluated when other functions are used like List[Unevaluated[{{5 + 6}, {7 + 8}}]] – Basheer Algohi Dec 03 '14 at 02:25
  • 1
    What your call "unclear" is the expected behavior. The cases like Unevaluated[{{5 + 6}, {7 + 8}}]*1 can be understood from Trace[Unevaluated[{{5 + 6}, {7 + 8}}]*1, TraceOriginal -> True]. What happens is that at the first step the Unevaluated is stripped off and without evaluation of its contents (as expected) and you get {{5 + 6}, {7 + 8}}*1. Now further evaluation rules (built-in) of Times are applied, consider this hand-made reconstruction of Times: times[x__] := times2[x]; Trace[ times[1, Unevaluated[{{5 + 6}, {7 + 8}}]], TraceOriginal -> True]. (continued) – Alexey Popkov Dec 03 '14 at 05:43
  • 1
    As you see, at the second step you have a new expression without Unevaluated which is evaluated in the usual way. Now check this: SetAttributes[times2, HoldAll];times[x__] := times2[x]; Trace[times[1, Unevaluated[{{5 + 6}, {7 + 8}}]], TraceOriginal -> True]. You see that if times2 has the HoldAll attribute you get almost the same result as without any evaluation rules defined: evaluation stops but in any case Unevaluated fires when the first evaluation rule fires. – Alexey Popkov Dec 03 '14 at 05:47
  • 1
    In the other words, Unevaluated is already stripped off at the first step when the first evaluation rule was applied. But what will happen if the evaluation rule must not be applied? Consider this: Clear[times]; times[x__]:=times2[x]/;False;Trace[times[1,Unevaluated[{{5+6},{7+8}}]],TraceOriginal->True]. You see that at some step the Unevaluated is stripped off but finally the original expression is returned. In other words, if the evaluation does not change the original expression, Unevaluated is not stripped off in the result. – Alexey Popkov Dec 03 '14 at 05:56
  • very clear. it is indeed an "(evaluation leek) inside of TreeForm". Even Trace[TreeForm[Unevaluated[{{5 + 6}, {7 + 8}}]],TraceOriginal -> True] can not capture the process how TreeForm works. The first element is indeed the final result of TreeForm[Unevaluated[{{5 + 6}, {7 + 8}}]]. The case is similar with Trace[FullForm[Unevaluated[{{5 + 6}, {7 + 8}}]],TraceOriginal -> True], however FullForm holds perfectly its argument unevaluated whereas TreeFrom is not. Thanks a lot:) – Basheer Algohi Dec 03 '14 at 07:04