Smooth animation of ListLinePlot

Question

I have a sequence of 2D-points from uniformly sampling a time dependent process and plot this sequence with ListLinePlot. For example:

data = Table[{Sin[x], x Cos[x]}, {x, 0, Pi, Pi/10}];
ListLinePlot[data, InterpolationOrder -> 2, Epilog -> Point@data]

I would like to animate the interpolated curve smoothly as a function of time. Here is what I tried:

i[t_] := {ListInterpolation[data[[All, 1]]][t],
  ListInterpolation[data[[All, 2]]][t]}
frames = Table[
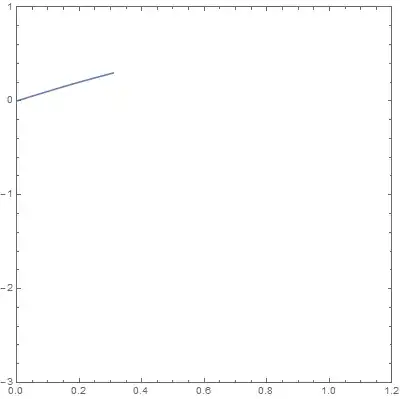
   ListLinePlot[Join[data[[1 ;; Floor@s]], {i[s]}], 
    InterpolationOrder -> 2, Axes -> None, ImageSize -> 400, 
    AspectRatio -> 1, PlotRange -> {{0, 1.2}, {-3, 1}}, 
    Frame -> True]
   ,{s, 2, 10, 0.2}];

The obvious problem with this approach is that the curve warps a lot in regions of high curvature. Ideally I would like the animation to perfectly coincide with the full plot at any timestep. Any ideas?

Use path length parametrization. You should be able to search for that in this site — Dr. belisarius, Nov 28 '14 at 15:37
Example http://mathematica.stackexchange.com/a/63961/193, but there are surely more — Dr. belisarius, Nov 28 '14 at 15:40

Karsten7 · Accepted Answer · 2014-12-01T11:51:32.463

data = Table[{x, {Sin[x], x Cos[x]}}, {x, 0, Pi, Pi/10}];
i = Interpolation[data, InterpolationOrder -> 2];
frames = Table[
   ParametricPlot[i[t], {t, 0, maxt}, AspectRatio -> 1, Axes -> None, ImageSize -> 400, 
     AspectRatio -> 1, PlotRange -> {{0, 1.2}, {-3, 1}}, Frame -> True], 
   {maxt, 0.2, Pi, 0.05}];

Or

data = Table[{Sin[x], x Cos[x]}, {x, 0, Pi, Pi/10}];
i[t_] = {ListInterpolation[data[[All, 1]], InterpolationOrder -> 2][t], 
         ListInterpolation[data[[All, 2]], InterpolationOrder -> 2][t]};
idata = Table[i[s], {s, 1, 10, 0.2}];
frames = Table[
   ListLinePlot[idata[[;; s]], Axes -> None, ImageSize -> 400, AspectRatio -> 1, 
     PlotRange -> {{0, 1.2}, {-3, 1}}, Frame -> True], 
   {s, 6, Length@idata}];

Smooth animation of ListLinePlot

1 Answers1