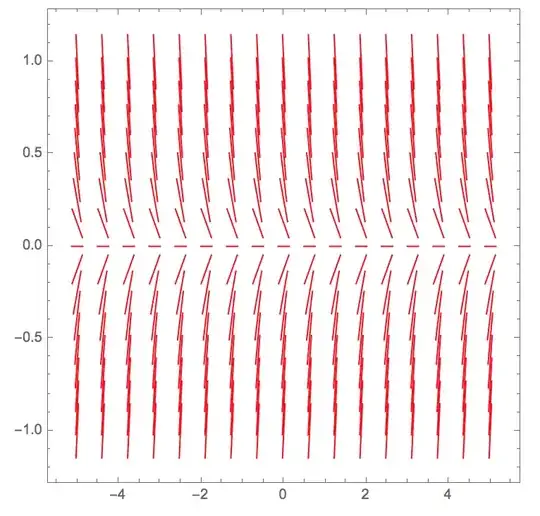
I want a slope field for a scalar differential equation. For simplicity I have chosen $dx/dt=rx$, where $r$ is a parameter. I used VectorPlot for the slope field as you can see from the code below. $|r|$ is bounded by 5. All is good when the PlotRange has the same horizontal and vertical ranges. Observe what happens when $a = 5$ and $b=1$. Unless the value of parameter $r$ is close to zero, the direction lines for a given $x$ value are so long that they spill over to the rows above and below.
Because this is a slope field and not a direction field for a 2D system, the length of the vectors should be constant. How can I achieve that? I have tried various rescaling and normalization but to no avail. Previous posts I've seen do not address this matter.
Thanks.
Manipulate[
VectorPlot[{1, r x}, {t, -a, a}, {x, -b, b}, VectorPoints -> 17,
VectorScale -> {0.03, Automatic, None},
VectorStyle -> {{Red, Arrowheads[0]}}],
{a, 1, 5},
{b, 1, 5},
{r, -5, 5}]



VectorScale? – murray Dec 03 '14 at 21:34