Lower branch of Lambert W function in mathematica

Question

I am interested in values of the Lambert W function, which is defined as the solution to the equation $ z = W(z) e^{W(z)} . $ The solution is not, however, single-valued, but branches into two solutions for $z < 0$. See for example the first figure in the Wikipedia page:

branches of the Lambert function

In Mathematica, I can get the part corresponding to the upper branch of the solution with ProductLog[z] and even different branches of it on the complex plane with ProductLog[k, z]. However, I don't find any way of computing the values of the lower branch of the solution to the equation above, i.e. the function that is, in the Wikipedia article, denoted as $W_{-1}(z)$. Is there a way to compute values of this function in Mathematica?

If, in MMA, k = 0 corresponds to the principal value, is ProductLog[-1, z] not the right thing? I've not looked it into this at all closely, just thinking out loud. Also, http://mathworld.wolfram.com/LambertW-Function.html — dr.blochwave, Dec 03 '14 at 09:39
Thank you! You are absolutely right. How stupid of me to miss this. I tried indices k=1,2,..., got some complex result and concluded that this is not what I want. Indeed, k=-1 seems to be the way to go (although I don't really understand this indexing). — Echows, Dec 03 '14 at 10:40
I'm not sure about it either...I've turned my comment into an answer for you :-) — dr.blochwave, Dec 03 '14 at 11:16
The indexing of the Lambert function $W_k(z)$ is analogous to the branches of the logarithm $\log(z)+2\pi i k$, with $k=0$ being the principal branches for both, and the positively-indexed branches being "stacked" on top of the principal branch, and similarly for the negatively-indexed ones. — J. M.'s missing motivation, May 04 '15 at 05:56

score 8 · Accepted Answer · answered Dec 03 '14 at 11:16

Expanding my comment into an answer, ProductLog can take two arguments, k and z, namely:

ProductLog[k, z]

There's some information to be found under the Details & Options of the documentation, but instead I turned to MathWorld, which has this to say on the matter:

The plot above shows the function along the real axis. The principal value of the Lambert W-function is implemented in Mathematica as ProductLog[z]. Different branches of the function are available in Mathematica as ProductLog[k, z], where k is any integer and k = 0 corresponds to the principal value. Although undocumented, LambertW[k, z] autoevaluates to ProductLog[k, z] in Mathematica.

Hence, if k = 0 gives the principal value, I think that using ProductLog[-1, z] should be the solution you're after for $W_{-1}(z)$.

I'm not sure why the documentation isn't as clear on this.

score 2 · Answer 2 · answered Dec 03 '14 at 10:05

Try this:

    lst = Select[
  Table[{z, (FindRoot[w + Log[w] == Log[z], {w, -1000, -1}, 
        Method -> "Secant", AccuracyGoal -> 3, PrecisionGoal -> 3] // 
       Chop)[[1, 2]]}, {z, -0.5, -0.009, 0.002}], Im[#[[2]]] == 0 &];

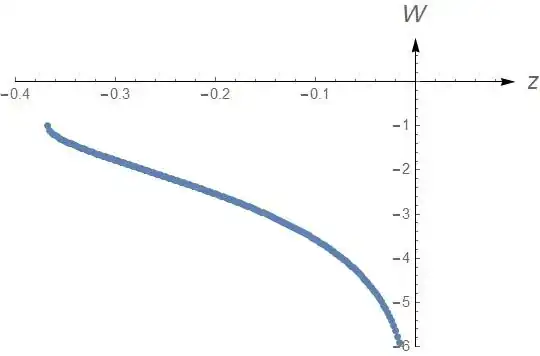
which gives the list with the structure {z,W}. This plots the list

    ListPlot[Select[lst, Im[#[[2]]] == 0 &], 
 PlotRange -> {{-0.4, 0.1}, {-6, 1}}, AxesStyle -> Arrowheads[0.03], 
 AxesLabel -> {Style["z", 16, Italic], Style["W", 16, Italic]}]

It should look like follows: enter image description here

There is a still more simple approach to this question. Just let us plot the function using the ParametricPlot:

 ParametricPlot[{W*Exp[W], W}, {W, -6, 0}, 
 PlotRange -> {{-0.4, 0.1}, {-6, 1}}, AspectRatio -> 0.6, 
 AxesStyle -> Arrowheads[0.03], 
 AxesLabel -> {Style["z", 16, Italic], Style["W", 16, Italic]}]

Obviously, it should look very close to the first one: enter image description here

If you need a table of the solution (e.g., zversus Wyou can make the list using the same idea:

lst2 = Table[{W*Exp[W], W} // N, {W, -6, 0, 0.3}]

yielding

(*  {{-0.0148725, -6.}, {-0.019072, -5.7}, {-0.0243895, -5.4}, \
{-0.0310934, -5.1}, {-0.0395028, -4.8}, {-0.0499905, -4.5}, \
{-0.0629814, -4.2}, {-0.0789435, -3.9}, {-0.0983654, -3.6}, \
{-0.121714, -3.3}, {-0.149361, -3.}, {-0.181455, -2.7}, {-0.217723, \
-2.4}, {-0.257158, -2.1}, {-0.297538, -1.8}, {-0.334695, -1.5}, \
{-0.361433, -1.2}, {-0.365913, -0.9}, {-0.329287, -0.6}, {-0.222245, \
-0.3}, {0., 0.}}   *)

I made a small step to have it short.

Have fun!

I'm sure this works, but unfortunately blochwave gave a much easier solution in the comments :). Thanks anyway. — Echows, Dec 03 '14 at 10:41

Lower branch of Lambert W function in mathematica

2 Answers2