observe since Cosh blows up the solutions are all near the zeros of the periodic Cos:
x /. # & /@
Flatten[Table[
FindRoot[ Cos[x] Cosh[x] - 1 , {x, Pi(1/2 + n)},
WorkingPrecision -> 20] , {n, 1, 100}]]
{4.7300407448627040260, 7.8532046240958375565, 10.995607838001670908, \
14.137165491257464177, 17.278759657399481438, 20.420352245626061091, \
23.561944902040455075, 26.703537555508186248, 29.845130209103254267, \
32.986722862692819562, 36.128315516282622650, 39.269908169872415463, \
42.411500823462208720, 45.553093477052001958, 48.694686130641795196, \
51.836278784231588435, 54.977871437821381673, 58.119464091411174912, \
61.261056745000968150, 64.402649398590761388, 67.544242052180554627, \
70.685834705770347865, 73.827427359360141104, 76.969020012949934342, \
80.110612666539727581, ....
(plus 0 .. and it is symmetric of course)
I suppose that's pretty close to where you started except make the table {3Pi/2,..,Pi}
Edit --- large x approximation:
asymp = Simplify[x /. First@Solve[
Simplify[ Normal@Series[ Cos[x] Cosh[x] ,
{x, Pi ( n + 1/2) , 1}] == 1,
Element[n, Integers]] , x ]]
(1/2 + n) Pi - (-1)^-n Sech[(1/2 + n) Pi ]
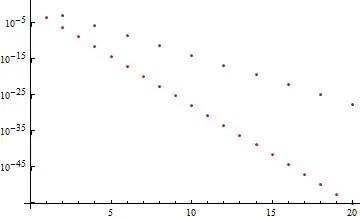
This shows the error in this approximation, as well as the error with simply using Pi(n+1/2)
Show[{
ListLogPlot[
Table[asymp - (x /. FindRoot[Cos[x] Cosh[x] - 1, {x, Pi (1/2 + n)} ,
WorkingPrecision -> 100]) , {n, 20}] , PlotStyle -> Red],
ListLogPlot[
Table[Pi ( n + 1/2) - (x /. FindRoot[Cos[x] Cosh[x] - 1, {x, Pi (1/2 + n)} ,
WorkingPrecision -> 100]) , {n, 20}] ]}]