Polar histogram

Question

I am developing an algorithm to generate a descriptor of a 2D object based on polar histogram. suppose that we have a datalist centered in {cx,cy}. I use 36 bins where I consider 12 angles and 3 different radius (see figure). I tried this code but I did not get the right figure. How can specify just 12 angles and how can we count the point of each sector?

data = {{10, 10}, {20, 20}, {40, 40}, {10, 20}, {100, 2}, {1, 1}, {2, 
    40}, {10, 11}, {12, 13}, {15, 15}, {100, 25}, {112, 12}, {113, 
    114}, {1, 111}};
center={50,50}
centereddata = (# - center) & /@ data;
angles = N[ArcTan[#[[1]], #[[2]]]/Degree] & /@ centereddata
radiis = N@Sqrt[#[[1]]^2 + #[[2]]^2] & /@ centereddata;
ListPolarPlot[Transpose[Join[{angles}, {radiis}]], PolarAxes -> True,
 PolarGridLines -> Automatic,PolarTicks -> {"Degrees", Automatic}]

Answer 1

 data = RandomReal[ {0, 200}, {200, 2}];
 center = {50, 50};
 centereddata = (# - center) & /@ data;
 angles = N[ArcTan[#[[1]], #[[2]]]/Degree] & /@ centereddata;
 radiis = N@Sqrt[#[[1]]^2 + #[[2]]^2] & /@ centereddata;

note you need to use Degree to put the angles back to radians here..

 polardata = Transpose[Join[{angles Degree}, {radiis}]];
 ListPolarPlot[polardata, PolarAxes -> True, 
    PolarGridLines -> Automatic, PolarTicks -> {"Degrees", Automatic}]

 bins = Table[a, {a, -180, 180, 30}];
 bincenters = ( Degree) Mean /@ Partition[ bins , 2, 1];
 hdata = Transpose[{bincenters , BinCounts[angles, {bins}] } ];
 ListPolarPlot[ hdata , PolarAxes -> True, PolarGridLines -> Automatic,
    PolarTicks -> {"Degrees", Automatic},
    Epilog -> {Red, 
    Line[{{0, 0}, #[[2]] {Cos[#[[1]]], Sin[#[[1]]]}}] & /@ hdata}]

ListPolarPlot doesn't evidently have a Filling option, hence the Epilog

... I hope you didn't just want this :)

   Histogram[ 1/Degree First /@ polardata  , {bins}]

edit a bit fancier..

 Epilog -> {Red, {Line[{{0, 0}, #[[2]] {Cos[#[[1]]], Sin[#[[1]]]}}], 
     Circle[{0, 0}, #[[2]], {#[[1]] - 15 Degree, #[[1]] + 15 Degree}]} & /@ 
     hdata}`

Answer 2

[Edited to correct the bin definition.]

You could use SectorChart. The trick is to ensure that your bin widths sum to 360° and that the first bin charted starts at zero.

Firstly, and borrowing shamelessly from @george2079's answer [and subsequent correction], define the bins:

bins = Table[a , {a, -180, 180, 30}];

Next create the sector chart data:

sData = RotateLeft[
  Tooltip[Join[Differences[#1], {#2}], {Mean[#1], #2}] & @@@ 
   Transpose[{Partition[bins, 2, 1], BinCounts[angles, {bins}]}], 
  FirstPosition[bins, 0] - 1]

{{30, 1}, {30, 8}, {30, 0}, {30, 0}, {30, 2}, {30, 1}, {30, 0}, {30, 1}, {30, 0}, {30, 0}, {30, 1}, {30, 0}}

There are several things going on here:

• We add a tooltip so that the each sector is labelled with the mid-point of the bin and the count,
• we calculate the width of each bin and
• we rotate the data such that the bin starting at zero is first in the list. Obviously this requires a bin edge at zero.

Finally chart it, adding axes, etc. and rotating the origin (thanks again @george2079):

SectorChart[sData, PolarGridLines -> Automatic, 
 PolarTicks -> {Automatic, None}, PolarAxes -> {True, False}, 
 SectorOrigin -> 0]

Answer 3

I propose an example silhouette descriptor based on a polar histogram. In my example histogram consits of 36 bins.

newBinCounts funtion

newBinCounts[angles_, bins_] := Module[{hist, sectorIndex}, (
       hist = BinCounts[angles, {bins}];
       sectorIndex = 
        Table[Flatten[
          Union[Position[angles, #] & /@ 
            Select[angles, bins[[i]] <= # < bins[[i + 1]] &]]], {i, 1, 
          Length[bins] - 1}];
       {hist, sectorIndex}
       )]

polarHistogram function

polarHistogram[regionOfInterest_, anglebins_] := 
 Module[{positionsWhitePixel, centroid, centeredpositionsWhitePixel, 
   angles, bins, raduis, bincenters, histData, sectorIndex, hData, 
   binrad, listOfRadius, listHist}, (

   positionsWhitePixel = 
    PixelValuePositions[regionOfInterest, White];

   Graphics[{Point@positionsWhitePixel}];

   centroid = N@Mean[positionsWhitePixel];


   centeredpositionsWhitePixel = (# - centroid) & /@ 
     positionsWhitePixel;

   angles = 
    Mod[(# + 360), 360] & /@ (N[ArcTan[#[[1]], #[[2]]]/Degree] & /@ 
       centeredpositionsWhitePixel);
   raduis = 
    N@Sqrt[#[[1]]^2 + #[[2]]^2] & /@ centeredpositionsWhitePixel;

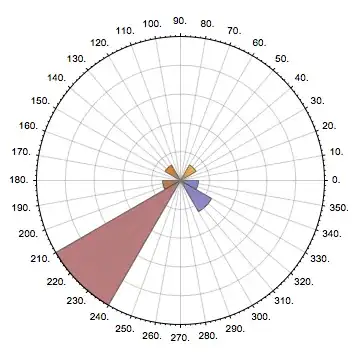
   Print[ListPolarPlot[Transpose[Join[{angles Degree}, {raduis}]], 
     PolarAxes -> True, PolarGridLines -> Automatic, 
     PolarTicks -> {"Degrees", Automatic}]];

     bins = Table[i, {i, 0, 360, anglebins}];
   bincenters = (Degree) Mean /@ Partition[bins, 2, 1];
   {histData, sectorIndex} = newBinCounts[angles, bins];
   hData = Transpose[{bincenters, BinCounts[angles, {bins}]}];

   Print[ListPolarPlot[hData, PolarAxes -> True, 
     PolarGridLines -> Automatic, 
     PolarTicks -> {"Degrees", Automatic}, 
     Epilog -> {Red, 
       Line[{{0, 0}, #[[2]] {Cos[#[[1]]], Sin[#[[1]]]}}] & /@ hData}]]
   (*in this code, i consider 3 raduis 0-20,
   20-40,40,200*)
   binrad = {0, 20, 40, 200};
   listOfRadius = raduis[[#]] & /@ sectorIndex;
   listHist = Transpose[BinCounts[#, {binrad}] & /@ listOfRadius];
   listHist
   )]

This function calculate an histogram of 36 bins. (call function using the silhouette)

list3 = polarHistogram[sil3, 30];


 (*list3={{100,103,104,107,104,99,111,104,106,103,104,111},{309,316,311,263,303,309,319,313,316,314,314,319},{1325,2079,132,0,45,359,1741,1674,514,148,53,176}}*)

\ https://i.stack.imgur.com/aZmWQ.png