10

I'm having a hard time getting FindInstance to return multiple results. Consider this simple example:

FindInstance[a > 0 && b >= 0 && c >= a + b && a >= c/3 , {a, b, c}, Integers, 2]

Mathematica (8.0.1 on Mac) quickly returns

{{a -> 244, b -> 206, c -> 618}, {a -> 306, b -> 299, c -> 860}}

Good. But if I change c/3 to c/4, which only relaxes the constraints, Mathematica goes busy for 18 sec. For a little more complicated case (9 variables with 15 similar constraints) it never returns (I left it running for several days).

Asking for one solution for the c/4 case (and for the 9 variable case) gets an immediate result: 

FindInstance[a > 0 && b >= 0 && c >= a + b && a >= c/4, { a, b, c}, Integers, 1]

returns

{{a -> 1, b -> 0, c -> 3}}

What accounts for the difference?

One more edit: for completeness, here's the 9 variable case:

FindInstance[{a0 >= 0, a1 >= 0, a2 >= 0, a3 >= 0, a4 >= 0, a5 >= 0, 
  a6 >= 0, a7 >= 0,
  nn == a0 + a2 + a4 + a6 + a1 + a3 + a5 + a7,
  (a1 + a3 + a5 + a7) / nn >= 0.5735, (a1 + a3 + a5 + a7) /nn  <= 0.5745,
  (a2 + a3 + a6 + a7) / nn >= 0.4715, (a2 + a3 + a6 + a7) / nn <= 0.4725,
  (a4 + a5 + a6 + a7) / nn >= 0.5225, (a4 + a5 + a6 + a7) / nn <=  0.5235,
  (a3 + a7)           / nn >= 0.2325, (a3 + a7)           / nn <= 0.2335,
  (a6 + a7)           / nn >= 0.2775, (a6 + a7)           / nn <= 0.2785,
  (a5 + a7)           / nn >= 0.2655, (a5 + a7)           / nn <= 0.2665,
  ( a7)               / nn >= 0.1195, (a7)                / nn <= 0.1205
  },
 {a0 , a1, a2, a3, a4, a5 , a6, a7, nn}, Integers, 2]

I tried a few variants, such as replacing the decimals with fractions and expanding nn, to no avail.

xan
  • 545
  • 2
  • 11
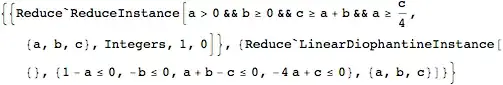
  • After 18 seconds I get {{a -> 343, b -> 570, c -> 1003}, {a -> 520, b -> 826, c -> 1648}} on mine (8.0 on win32). – wxffles Jun 14 '12 at 01:27
  • Yeah, me too (same configuration as wxffles) – Dr. belisarius Jun 14 '12 at 01:35
  • @wxffles thanks for trying it. I updated the Q. After the bigger problem took days I started equating 5 seconds with infinity. I do get an answer after 18 secs, too. Still, I wonder what makes the 3 -> 4 change take so much longer. – xan Jun 14 '12 at 02:27
  • 1
    Related: http://mathematica.stackexchange.com/q/3554/121 – Mr.Wizard Jun 14 '12 at 12:24

3 Answers3

7

When requesting multiple instances larger values for each variable are produced:

FindInstance[a > 0 && b >= 0 && c >= a + b && a >= c/4, {a, b, c}, Integers, 5]

{{a -> 536, b -> 909, c -> 1960},
 {a -> 353, b -> 420, c -> 1237},
 {a -> 403, b -> 762, c -> 1472},
 {a -> 709, b -> 933, c -> 2337},
 {a -> 543, b -> 956, c -> 2040}}

I suspect this larger search space is the reason for the slow behavior. There may be an option that controls this but I am not aware of it. I have a couple of ideas for working around this.

Get one instance at a time

The idea here is to restrict the set to exclude each solution as it is found, then ask for one instance.

par = {a > 0, b >= 0, c >= a + b, a >= c/4};

f = Or @@ Unequal @@@ 
  First@FindInstance[par~Join~#, {a, b, c}, Integers, 1] &;

List @@ Rule @@@ # & /@ Nest[Append[#, f@#] &, {f@par}, 7]

{{a -> 1, b -> 0, c -> 3}, {a -> 2, b -> 0, c -> 4}, {a -> 3, b -> 0, c -> 5},
 {a -> 4, b -> 0, c -> 6}, {a -> 2, b -> 1, c -> 5}, {a -> 2, b -> 0, c -> 3},
 {a -> 3, b -> 0, c -> 3}, {a -> 2, b -> 1, c -> 4}}

These results are produced much more quickly, again I suspect because of a smaller search space.

Add an upper bound

With knowledge that solutions are possible with small values:

par2 = {15 > a > 0, 15 > b >= 0, 15 > c >= a + b, 15 > a >= c/4};

FindInstance[par2, {a, b, c}, Integers, 100] // Length // Timing

{0.016, 100}

So 100 solutions may be found almost instantly within the restricted space.

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
3

You may also use Reduce previously to simplify (and somewhat generalize) your problem.

r[n_Integer] := Evaluate@Reduce[a > 0 && b >= 0 && c >= a + b && a >= c/n, {a, b, c}, Integers];
FindInstance[r[4], {a, b, c}, 100]

The answer is very quick.

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
  • Great answer. I'm a bit annoyed with myself for not trying that. Nevertheless I know from past experience there are times it does not help, and other measures are required to coax results from FindInstance. – Mr.Wizard Jun 14 '12 at 14:11
  • By the way you can use Set and drop the Evaluate@. – Mr.Wizard Jun 14 '12 at 14:13
  • @Mr.Wizard You are right. Also, if you examine the output of Reduce[a > 0 && b >= 0 && c >= a + b && a >= c/n, {a, b, c}, Integers] , you will see that this time Evaluate[] is luckily finding a neat expression for Integer and positive n. – Dr. belisarius Jun 14 '12 at 14:15
1

It seems FindInstance uses different methods to find 1 instance and to find more than one instance.

constraint = {a > 0, b >= 0, c >= a + b, a >= c/4};

Trace[
 FindInstance[constraint, {a, b, c}, Integers, 1],
 _Reduce`LinearDiophantineInstance | _Reduce`ReduceInstance,
 TraceInternal -> True
 ]

Mathematica graphics

Trace[
 FindInstance[constraint, {a, b, c}, Integers, 2],
 _Reduce`LinearDiophantineInstance | _Reduce`ReduceInstance,
 TraceInternal -> True
 ]

Mathematica graphics

LinearDiophantineInstance returns quickly, even on the 9-variable problem. The second call to ReduceInstance in the 2-instance case takes a long time, which is easy to believe given the complexity of the auxiliary system. In the 9-variable case, I only waited a few minutes while, I assume, it was building the argument for a second ReduceInstance call.

I do not know whether there is a reason to use ReduceInstance instead of nested calls to LinearDiophantineInstance, similar to Mr.Wizard's approach. Given that it handles both of the examples, it seems unlikely.

Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747