I'm having trouble understanding why the following RegionPlot code produces results:
pred[x_, y_] :=
0 < x <= 0.5 ∧ EvenQ@Floor[(y - 0.05)/0.1] ∨
0.5 < x < 1 ∧ EvenQ@Floor[y/0.1]
RegionPlot[pred[x, y], {x, 0, 1}, {y, 0, 1},
PlotRange -> {{0, 1}, {0, 1}}, PlotPoints -> 100]
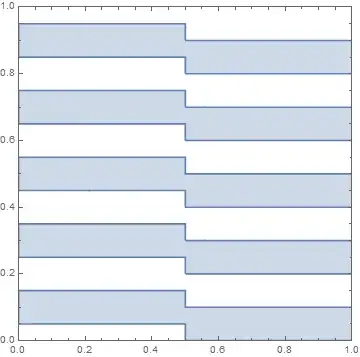
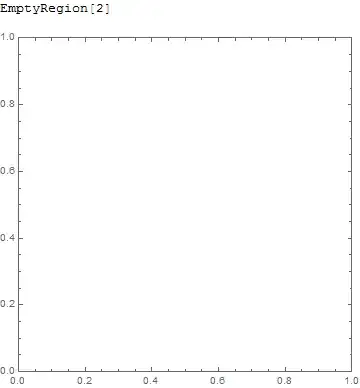
while this code using ImplicitRegion produces an empty region:
Ω1 =
ImplicitRegion[
0 < x <= 0.5 ∧ EvenQ@Floor[(y - 0.05)/0.1] ∨
0.5 < x < 1 ∧ EvenQ@Floor[y/0.1], {{x, 0, 1}, {y, 0, 1}}]
RegionPlot[
RegionMember[Ω1, {x, y}], {x, 0, 1}, {y, 0, 1},
PlotRange -> {{0, 1}, {0, 1}}, PlotPoints -> 100]
It appears related to the use of EvenQ. So a possible workaround might be replacing with Mod[#,2]==0&.
Mod[#,2]==0&? Wondering about the "might". Also, region functionality should be getting a significant update in V10.0.2, which seems to be out (I don't have access yet). I can confirm this problem exists in V10.0.1. – Michael E2 Dec 11 '14 at 18:15ImplicitRegionevaluatesEvenQon symbolic input, which returnsFalse, since an expression with a symbol is not an even integral. – Michael E2 Dec 11 '14 at 18:20Modisn't a perfect solution. It still produces anImplicitRegionthat isn't plottable directly. Further, what attribute doesEvenQhave thatEqualdoes not, such thatEqual[x, 3]remains unevaluated whileEvenQ[x]givesFalse? – Jason B. Jan 05 '16 at 13:58Qwill always returnTrueorFalse. AFAIK, this is done programmatically (not throughAttributesper se, if that's what you meant by attributes). For example, if you wanted anEqualQ, you could useTrueQ@ Equal[x, 3], which would returnFalseifEqual[x, 3]does not evaluate toTrue. (This Q property means, for instance, that you can countIfevaluating one of its next two arguments and so forth.) – Michael E2 Jan 05 '16 at 14:44{x, y} \[Element] Realsto yourpredallowsDiscretizeRegion[\[CapitalOmega]]to work (but still notRegionPlot). One issue seems to be thaty == 1contains a boundary of a segment that lies abovey == 1. If you change theImplicitRegionto{y, 0, 0.999}and add the{x, y} \[Element] Reals,RegionPlotworks. -- You can also add the condition0 <= y < 1topred. – Michael E2 Jan 05 '16 at 14:53