How would I rotate a table of Cuboids around the y axis?

Question

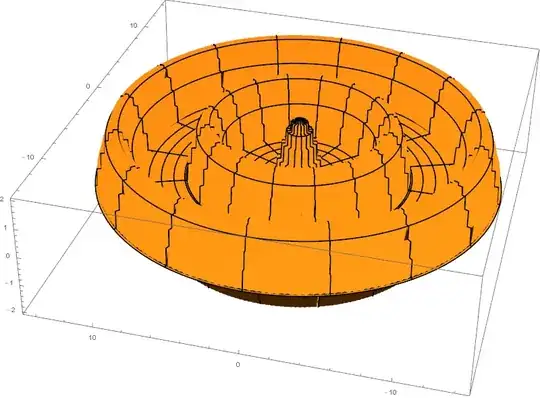
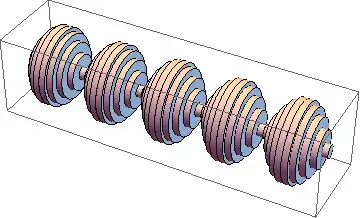
Currently I can print out this using Graphics3d: Graph Here's the code:

a = (-5 \[Pi])/2;
b = (5 \[Pi])/2;
dx = (b - a)/50;
f[x_] := 2 Cos[x];
startpos[1, k_] := a + (k - 1) dx;
startpos[2, k_] := a + k*dx;
startpos[3, k_] := a + (2 k - 1)/2 dx;

model = Graphics3D[{Table[
Cuboid[{{a + (l - 1) dx, 0, 0}, {a + l*dx, +.01, 
   f[startpos[3, l]] + .01}}], {l, 1, 50, 1}]}];

Show[model]

I want to rotate it around the y-axis. I already tried using RevolutionPlot3d, but I'm not sure how to set it up exactly. Here's my failed attempt:

model = RevolutionPlot3D[{Table[
 Cuboid[{{a + (l - 1) dx, 0, 0}, {a + l*dx, +.01, 
    f[startpos[3, l]] + .01}}], {l, 1, 50, 1}]}, {x, a, b}, 
RevolutionAxis -> "Y", AspectRatio -> Automatic, Mesh -> None, 
BoundaryStyle -> Black, PlotStyle -> Thickness[.1]] ;
Show[model]

Do you want a surface of revolution? Or do you simply want to enable rotation of the cuboids? — DavidC, Dec 12 '14 at 13:42

Kuba · Accepted Answer · 2014-12-12T13:34:41.680

2

I would switch approach to something like:

Show[
     RevolutionPlot3D[2 Cos[Floor[x, (Pi/10)]], {x, 0, 9 Pi/2 + .2}, 
                      Exclusions -> None, PlotPoints -> 100, MeshStyle -> Thick],
     RevolutionPlot3D[0, {x, 0, 9 Pi/2}, Exclusions -> None, 
                                         PlotPoints -> 50, MeshStyle -> Thick]
     ,
     ImageSize -> 800]

enter image description here

edited Dec 12 '14 at 13:34

answered Dec 12 '14 at 08:38

Kuba

136,707
13
279
740

Your first version acutely reminded me of a Guglhupf (yum)! Please roll back to the delicious seasonal function. – Yves Klett Dec 12 '14 at 15:11
1

@YvesKlett Wow, that name sounds like a joke :) But yum indeed ;) – Kuba Dec 13 '14 at 21:30

score 1 · Answer 2 · answered Dec 12 '14 at 10:39

Firstly, no need to use Show, simply remove the ; from the end of your Graphics3D expressions.

Secondly, try evaluating:

Graphics3D[
 Table[Cuboid[{{a + (l - 1) dx, 0, 0}, {a + l*dx, +.01, 
     f[startpos[3, l]] + .01}}], {l, 1, 50, 1}], 
 AxesLabel -> {x, y, z}, Axes -> True, BoxRatios -> 1, Ticks -> None, 
 AxesOrigin -> {0, 0, 0}, Boxed -> False, 
 AxesStyle -> Directive[Orange, 12]]

Orientation plot

Are you sure you want to rotate it about the y-axis? Isn't it going to be a mess?

I suspect you mean the x-axis, in which case basically you want to replace Cuboid[{{x0,0,0},{x1,y1,z1}}] -> Cylinder[{{x0,0,0},{x1,0,0}},Abs[z1]]. (And forget about RevolutionPlot3D which creates surfaces of revolution rather than revolving graphics primitives.)

model = Graphics3D[
  Table[Cylinder[{{a + (l - 1) dx, 0, 0}, {a + l*dx, 0, 0}}, 
    Abs[f[startpos[3, l]]]], {l, 1, 50}]]

Rotated plot

OP said y but I think he meant z. But not x. Maybe you are right, I don't know... :) — Kuba, Dec 12 '14 at 10:43
@Kuba You're bound to be correct, that's the more difficult axis! — MikeLimaOscar, Dec 12 '14 at 11:40

How would I rotate a table of Cuboids around the y axis?

2 Answers2