1

I would like to calculate the normal at a certain point of a parabola. The parabola is defined only on a certain area according to a Piecewise function. Afterwards I would like to add the normal to the coordinate of the parabola for making a graph. 

    {0.3, 1, 1.09} 
    {-0.6, -2, 1}

Sum of both vectors according to Mathematica:

    {{-0.3, -1.7, 1.3}, {0.4, -1, 2}, {0.49, -0.91, 2.09}}

Of course this should only contain three elements: normal in {x,y,z} direction.

Below you can find the full code. Why does Mathematica give 3x3 values (instead of 1x3) here?

 func[u_, v_] := u^2 + v^2
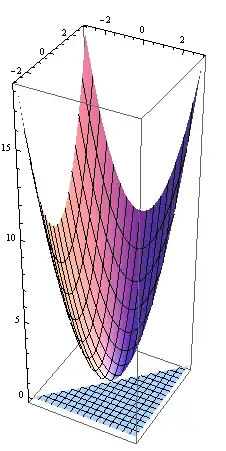
 parabola = {u, v,
   Piecewise[
    {
     {func[u, v], u < v}
     }, 0
    ]
   }
 ParametricPlot3D[parabola, {u, -3, 3}, {v, -3, 3}]

 normal = Piecewise[
    {{Cross[
       D[{u, v, func[u, v]}, u],
       D[{u, v, func[u, v]}, v]],
      u < v}}
    ];
 normal + parabola;
 repl = {u -> 1, v -> 1};
 parabola /. repl
 normal /. repl
 normal + parabola /. repl


 repl = {u -> .3, v -> 1};
 parabola /. repl
 normal /. repl
 normal + parabola /. repl (*Wrong Output*)

Here the output is:

{1, 1, 0}

0

{1, 1, 0}

{0.3, 1, 1.09}

{-0.6, -2, 1}

{{-0.3, -1.7, 1.3}, {0.4, -1, 2}, {0.49, -0.91, 2.09}}

enter image description here

LvD
  • 55
  • 5
  • 3
    Is this what you mean? (normal /. repl) + (parabola /. repl) The way you have written it, it first adds normal+parabola (which is the larger expression) and then substitutes repl. This is where the matrix comes from. – bill s Dec 24 '14 at 15:47

1 Answers1

1

To elaborate on the comment by @bills, parabola is a List of three elements

parabola // InputForm
{* {u, v, Piecewise[{{u^2 + v^2, u < v}}, 0]} *)

whereas normal is a single function containing a List

normal // InputForm
(* Piecewise[{{{-2*u, -2*v, 1}, u < v}}, 0] *)

Consequently, Mathematica dutifully adds that single element of normal to each of the three elements of parabola, yielding

normal + parabola // InputForm
(* {u + Piecewise[{{{-2*u, -2*v, 1}, u < v}}, 0], 
 v + Piecewise[{{{-2*u, -2*v, 1}, u < v}}, 0], 
 Piecewise[{{u^2 + v^2, u < v}}, 0] + Piecewise[{{{-2*u, -2*v, 1}, u < v}}, 0]} *)

To successfully add the two expressions, you must put them in the same form. The method given by @bills is one way. Another is the redefine parabola as

parabola2 = Piecewise[{{{u, v, func[u, v]}, u < v}}, 0]

for which

normal + parabola2 /. repl
(* {-0.3,-1,2.09} *)
bbgodfrey
  • 61,439
  • 17
  • 89
  • 156