How to prevent instability blow up in NDSolve?

Question

I have the following code to solve a PDE:

e = 2.5;
xmax = 5;
ymax = 5;
sol[x_, y_] = f[x, y] /. First@NDSolve[{
     -D[f[x, y], x, x] - D[f[x, y], y, y] == e f[x, y],
     Derivative[0, 1][f][x, -ymax] == Cos[\[Pi]/(2 xmax) x],
     f[x, -ymax] == 0,
     f[-xmax, y] == 0,
     f[xmax, y] == 0
     }, f[x, y], {x, -xmax, xmax}, {y, -ymax, ymax}]

I'd expect to get a Sin[]-like solution in y direction, but what I get instead is this:

Plot3D[sol[x, y], {x, -xmax, xmax}, {y, -ymax, ymax}, PlotRange -> {-1, 1}, AxesLabel -> {"x", "y", "f"},  MaxRecursion -> 3]

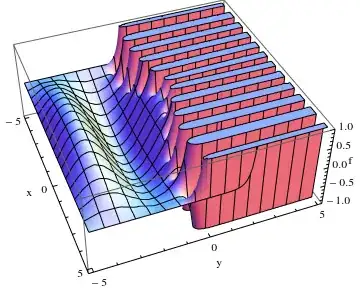
enter image description here

If I try using something like MaxStepSize -> 0.25, then the blow-up is just more frequent in x direction, and becomes visible at even smaller y values:

enter image description here

What can I do to prevent this blow-up and make NDSolve give the expected solution?

EDIT

In fact, the problem above is a minimal example showing the instability. What I'd actually like to solve is the equation with additional +U[x,y]f[x,y] on the LHS, where U[x,y]=-70Exp[-x^2-y^2]. I.e. the equation would look like

-D[f[x, y],x,x]-D[f[x,y],y,y]-70Exp[-x^2-y^2]f[x,y]==e f[x,y]

So, the answer I'm looking for should be extensible to this case. The answer by @xzczd solves the problem with minimal example, but unfortunately fails to extend to this one.

Just a check. Do you mean to have both second derivative terms as negative? If you are trying to solve the wave equation then the first one should be positive. If both are negative then the solutions may blow up. Changing the sign of the first term gives a good solution. — Hugh, Dec 29 '14 at 13:12
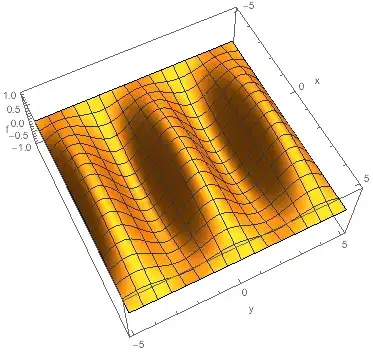
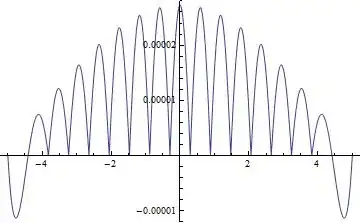
@Hugh no, the equation is as intended, with both derivatives negative. I do understand that solutions could blow up in some circumstances (e.g. when e<0), but in this case the solution NDSolve gives blows up with the frequency of the grid, so in the limit of infinite grid density the function won't be differentiable, which doesn't look right. — Ruslan, Dec 29 '14 at 13:44
As bbgodfrey pointed out, many finite-difference-based methods actually become less stable when a finer grid is used, rather than more stable (this tends to surprise people, as intuition suggests using a finer grid will usually make things better, not worse). One solution is to use other methods, like Michael E2's suggestion. There might be other ways, too, but I'm not very knowledgeable here. — DumpsterDoofus, Dec 30 '14 at 00:10
Just a side note, today I came across this article and noticed your problem is actually ill-posed. Still, a quick search shows there seems to be several techniques to deal with it, but sadly I can't understand those materials I found… — xzczd, Sep 25 '16 at 07:09

score 9 · Answer 1 · answered Dec 29 '14 at 18:15

9

The Finite Element Method seems more stable for this type of problem.

e = 2.5;
xmax = 5;
ymax = 5;
sol = First@
   NDSolve[{-D[f[x, y], x, x] - D[f[x, y], y, y] + NeumannValue[Cos[\[Pi]/(2 xmax) x], y == -ymax] == e f[x, y], 
     DirichletCondition[f[x, y] == 0, y > -ymax]}, 
    f, {x, -xmax, xmax}, {y, -ymax, ymax}, 
    Method -> {"FiniteElement", "MeshOptions" -> {MaxCellMeasure -> 0.01}}];

Plot3D[f[x, y] /. sol, {x, -xmax, xmax}, {y, -ymax, ymax}, 
 PlotRange -> {-1, 1}, AxesLabel -> {"x", "y", "f"}, PlotPoints -> 101]

Mathematica graphics

We can use "MeshOptions" to control the quality of the solution (as described in the linked tutorial above). Comparing the boundary condition along y == -ymax, we see that MaxCellMeasure -> 0.01 helps to meet the condition much better than the default of 0.25:

Plot[{Cos[π/(2 xmax) x], D[f[x, y], y] /. sol /. y -> -ymax} // Evaluate, {x, -xmax, xmax}]

Mathematica graphics

I hope it works in your actual use case! :)

answered Dec 29 '14 at 18:15

Michael E2

235,386
17
334
747

This is a great answer. Would you know why the default method does not check its convergence and falls back onto this solution? It makes using NDSolve hazardous that no such validation is carried out? – chris Dec 29 '14 at 19:38
@MichaelE2 unfortunately it requires Mathematica 10. Still interesting anyway. What would be the way to add U[x,y]f[x,y] to the LHS of the equation with this awkward Neumann condition syntax? – Ruslan Dec 29 '14 at 19:46
@Ruslan I think there might be a way to do FEM in V9....I'm not sure how much work it would take. See for instance Jens' answer here. – Michael E2 Dec 29 '14 at 20:20
@chris Thanks. I don't know how NDSolve chooses the method. It may have to do with the OP's setup. Someone from WRI might see your comment and be able to respond. – Michael E2 Dec 29 '14 at 20:24
It seems your formulation of the problem is not the same as the one in the OP. See wave equation section in the tutorial you linked. The problem in the OP basically only differs by a sign in a derivative (and other minor parts). But there's no NeumannValue[] used in the problem setup in that tutorial. And when I try to add a U[x,y]f[x,y] term to the LHS of the equation with your formulation, I get completely wrong results, which don't even satisfy initial conditions. (I used U[x,y]=-70Exp[-x^2-y^2]). Are you sure your formulation is equivalent to mine? – Ruslan Dec 30 '14 at 07:33
@Ruslan How do you account for the boundary condition Derivative[0, 1][f][x, -ymax] == Cos[\[Pi]/(2 xmax) x]? That's what the NeumannValue is for. For the PDE -D[f[x, y], x, x] - D[f[x, y], y, y] + 70 Exp[-x^2 - y^2] f[x, y] + NeumannValue[Cos[\[Pi]/(2 xmax) x], y == -ymax] == e f[x, y], with the same Dirichlet condition, I get this: Mathematica graphics And it seems to me that all the BCs are satisfied, Neumann and Dirichlet. It's possible I've made a mistake somewhere, but I don't see any inconsistency yet. – Michael E2 Dec 30 '14 at 08:09
See In[50] and In[51] in the tutorial section I linked to. The latter is how I'd account for it. Am I wrong? And yes, the initial condition for derivative is not satisfied in your plot. In fact, even for the value of function at $y=-5$. – Ruslan Dec 30 '14 at 08:11
Let us continue this discussion in chat. – Michael E2 Dec 30 '14 at 16:20

bbgodfrey · Answer 2 · 2014-12-29T14:09:56.847

7

Your calculation is unstable, because the Courant limit is violated. For a square mesh, it is e > 4 dx^-2. Choosing e=27.5 gives

e=7.5 solution

edited Dec 29 '14 at 14:09

answered Dec 29 '14 at 14:04

bbgodfrey

61,439
17
89
156

So, what are the workarounds? Maybe some way to use rectangular mesh or some special Method of NDSolve? – Ruslan Dec 29 '14 at 14:20
The equation can be solved analytically, although I have not been able to coax DSolve to do it yet.. – bbgodfrey Dec 29 '14 at 14:28
Of course it can! But the equations I'm going to solve after fixing the stability problem can't! I just gave a minimal working example. – Ruslan Dec 29 '14 at 14:30
What is actual equation you are trying to solve? Courant limits sometimes are sensitive to details. – bbgodfrey Dec 29 '14 at 14:32
Add U[x,y]f[x,y] on the LHS of the equation where U[x,y] is some function, and e>U[x,y], then it's the equation I'm trying to solve. Restricting values of e beyond this is not a solution, of course. – Ruslan Dec 29 '14 at 14:33
I would try a standard finite difference discretization to create a set of algebraic equations in f at the mesh points, then use a Mathematica linear equation solver to obtain the answer. Probably, LinearSolve. – bbgodfrey Dec 29 '14 at 14:51
You also might add a first order time derivative to the equation to turn it into a diffusion equation, choose a reasonable initial condition, and run the calculation forward in time until it reaches steady state. – bbgodfrey Dec 29 '14 at 15:07

score 4 · Answer 3 · edited Apr 13 '17 at 12:56

Somewhat inspired by bbgodfrey's answer, after rereading the tutorial of "MethodOfLines", I found that a restriction for "MaxPoints" together with "DifferenceOrder" -> 2 solved the problem, no v10-feature is needed!:

e = 2.5;
xmax = 5;
ymax = 5;
sol[x_, y_] = 
 f[x, y] /. 
  With[{n = 18}, 
   First@NDSolve[{-D[f[x, y], x, x] - D[f[x, y], y, y] == e f[x, y], 
      Derivative[0, 1][f][x, -ymax] == Cos[π/(2 xmax) x], 
      f[x, -ymax] == 0, f[-xmax, y] == 0, f[xmax, y] == 0}, 
     f[x, y], {x, -xmax, xmax}, {y, -ymax, ymax}, 
     InterpolationOrder -> All, 
     Method -> {"MethodOfLines", 
       "SpatialDiscretization" -> {"TensorProductGrid", 
         "MaxPoints" -> n, "MinPoints" -> n, 
         "DifferenceOrder" -> 2}}]]

Plot3D[sol[x, y], {x, -xmax, xmax}, {y, -ymax, ymax}, AxesLabel -> {"x", "y", "f"}]
Plot[{Cos[π/(2 xmax) x] - D[sol[x, y], y] /. y -> -ymax} // Evaluate, {x, -xmax, xmax}]

enter image description here

Notice that "MinPoints" option isn't necessary here, but I found it lowers the error, at least at the boundary. And actually if you choose n = 10, "DifferenceOrder -> 2" can be eliminated, too, though a warning will be generated.

Great! But I can't seem to extend this to the equation with +U[x,y]f[x,y] on the LHS, where U[x,y]=-70Exp[-x^2-y^2]. I try to increase n, increase difference order, but still the blow up appears at about y==0 or earlier. — Ruslan, Dec 31 '14 at 08:32
@Ruslan If this method would have any chance to work, it should be decreasing rather than increasing n or "DifferenceOrder", sadly it seems that decreasing doesn't work either 囧. — xzczd, Dec 31 '14 at 14:29

How to prevent instability blow up in NDSolve?

3 Answers3

Linked