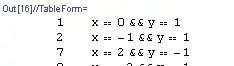Diophantine equation: getting a list of solutions for each coeficient

Question

I'm trying to solve the following diophantine equation,$$x^3+dy^3=1$$

such that $$x,y \in \mathbb{Z} \land y \neq 0$$

and I want to form a list of solutions for each $$d\in[1,1000]; d\in\mathbb{N}$$

I wrote

lista = Function[{d, i}, 
    FindInstance[x^3 + d*y^3 == 1 && y != 0, {x, y}, Integers, 
    i] /. {x -> a_, y -> b_} -> {a, b}];

module[{i, d, la, lb, r, rf},
d = 0; rf = {};
While[d <= 1000,
    d++; i = 0; r = {}; la = 1; lb = 2;
     While[lb > la,
     i++;
     la = Length[r];
     r = lista[d, i];
     lb = Length[r]];
     rf = Append[rf, {r, d}]]; rf]

But I'm not getting any success. Any help would be appreciated!

Edit: Belisarius' answer does what I would need it to, but can't be run nearly up to 1000. Anyone have an idea for a diferent approach?

Begin with Wolfram documentation, along with the 20 or questions in SE on this subject. — bbgodfrey, Jan 03 '15 at 19:59
I have read the documentation, and some of those questions. I posted this here mainly because I wanted to know what was wrong with my approach. I wouldn't have had I found the solution anywhere I looked before coming here. I'm going to investigate further on the previous questions about diophantine equations on here though. Thanks. — SilverShad0wz, Jan 03 '15 at 21:55

Dr. belisarius · Answer 1 · 2015-01-03T20:32:26.153

6

Complete brute force. Not guaranteed to run up to 1000 in a reasonable time frame:

Select[Table[{d, Reduce[x^3 + d y^3 == 1 && y != 00, {x, y}, Integers]}, {d, 1, 30}], 
       #[[2]] =!= False &] // TableForm

Mathematica graphics

edited Jan 03 '15 at 20:32

answered Jan 03 '15 at 20:25

Dr. belisarius

115,881
13
203
453

2

In fact, I can confirm now it won't run up to 1000 in an average human lifetime. Are you human? – Dr. belisarius Jan 03 '15 at 20:42
I am indeed human... so that'll be a problem hahaha. Thanks a lot for the approach suggestion though! – SilverShad0wz Jan 03 '15 at 21:51
On another note: wouldn't there be multiple solutions for each $d$? – SilverShad0wz Jan 03 '15 at 21:57
@SilverShad0wz Reduce finds the full solution set, not just one instance. This also means you can't trust it to return the result always in simple x == 0 && y == 1 form. – kirma Jan 04 '15 at 16:21
@kirma aaah, now I understand. Thanks! – SilverShad0wz Jan 04 '15 at 19:28

score 4 · Accepted Answer · answered Jan 04 '15 at 16:34

The equation $x^3+d~y^3=1$ becomes $x^3\equiv 1$, mod $d$. Hence, PowerModList[1,1/3,d] gives a list of all positive $x$ between 1 and $d-1$, inclusive, which satisfy $x^3\equiv 1$, mod $d$. For example, $d=20$ implies $x\equiv 1$, mod 20, is the only solution for $x$ between 1 and $d-1=19$. Adding and subtracting multiples of the modulus $d$ gives other valid solutions as $x\rightarrow...,-59,-39,-19,1,21,41...$. In the case of $d=7$, valid solutions are $x\equiv \{1,2,4\}$, mod 7. Adding and subtracting multiples of $d$ gives other solutions as $x\rightarrow...,-6,-5,-3,1,2,4,8,9,...$.

The strategy is to use PowerModList to find base solutions for $x$, extend the solutions by adding multiples of modulus $d$, find the corresponding solutions for $y=((1-x^3)/d)^{1/3}$, and test these candidate $y$ for integers not equal to zero.

DiophantineCubic[d_] := 
   Block[{a, x},
         a = PowerModList[1, 1/3, d];
         x = Sort[Flatten[Map[# + a &, d*Range[-5, 5]]]];
         Thread[{d, 
            Select[Transpose[{x, (1 - x^3)^(1/3)/d^(1/3)}] /.(-1)^(1/3)->-1,
                   IntegerQ[#[[2]]] && #[[2]] != 0 &]}]
   ]
   SetAttributes[DiophantineCubic, Listable]

When a solution for given $d$ exists, it seems to be unique. The Range[-5,5] statement is a total guess. For negative $x$, is seems -d+PowerModList[1,1/3,d] is all that is required.

There appear to be 32 values $d$ between 1 and 1000 each having a unique solution. It takes 1.5 s to find these on my machine (less than my average lifetime...).

The values of $d$ are: ${1, 2, 7, 9, 17, 19, 20, 26, 28, 37, 43, 63, 65, 91, 124, 126, 182, \ 215, 217, 254, 342, 344, 422, 511, 513, 614, 635, 651, 728, 730, 813, \ 999}$.

Diophantine equation: getting a list of solutions for each coeficient

2 Answers2