Let mathematica combine integral limits

Question

Is there a way to teach mathematica to combine integral limits according to $\int_a^b f dx+\int_b^c f dx=\int_a^cf dx$ to simplify expressions like $\int_0^1 f[t] dt+\int_1^x (1+f[t]) dt$ to $\int_0^t f[t] dt+x-1$ ? Additionally, it'll be helpful for mathematica to know $-\int_b^a f dx+\int_b^c f dx=\int_a^cf dx$ is equvalent to $\int_a^b f dx+\int_b^c f dx=\int_a^cf dx$.

Answer 1

You're looking for TagSetDelayed I believe:

Unprotect@Integrate;
Integrate /: 
  Plus[Integrate[ft_, {t_, a_, b_}], Integrate[ft_, {t_, b_, c_}]] := 
  Integrate[ft, {t, a, c}];
Integrate /: 
  Plus[Integrate[ft_, {t_, b_, a_}], Integrate[ft_, {t_, b_, c_}]] := 
  Integrate[ft, {t, a, c}];
Protect@Integrate;

But be careful when you unprotect system functions...

Answer 2

One may also use Inactivate/Activateconstruct. For example, try this

expr = Inactivate[
  Integrate[f[x], {x, 0, 1}] + Integrate[f[x], {x, 1, 2}], Integrate]

yielding this:

Then make the replacement:

    expr /. Inactivate[
   Integrate[g_, {x, a_, b_}] + Integrate[g_, {x, b_, c_}], 
   Integrate] -> Inactivate[Integrate[g, {x, a, c}], Integrate]

giving this:

Then let us activate the result:

 % // Activate

returning this:

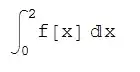
Let us also check it with a certain function f[x], say, with x^2:

 expr1 = Inactivate[
  Integrate[x^2, {x, 0, 1}] + Integrate[x^2, {x, 1, 2}], Integrate]

expr1 /. Inactivate[
   Integrate[g_, {x, a_, b_}] + Integrate[g_, {x, b_, c_}], 
   Integrate] -> Inactivate[Integrate[g, {x, a, c}], Integrate]

   % // Activate

(*  8/3 *)

Have fun!