Visualizing 3×3 spectrahedra

Question

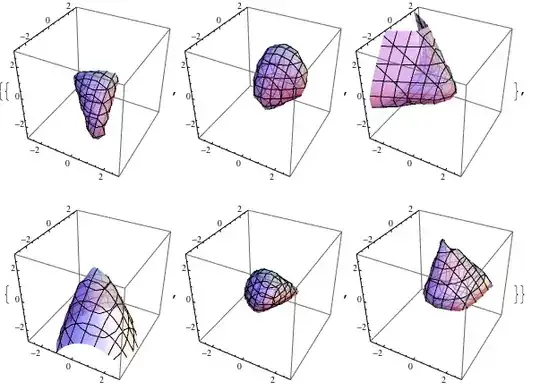
I'm trying to visualize the SDP cone over 3×3 matrices by plotting random 3D sections of it. Since each region is a system of inequality constraints, I'm using RegionPlot, but I think the plots would look better if they only showed the surface... what is a good way to achieve this?

spectro2 := (
   X = ( {
      {x1, x2, x3},
      {x2, x4, x5},
      {x3, x5, x6}
     } );
   vars = Union@Flatten@X;
   dvars = {x, y, z};
   m = Length@vars;
   n = Length@dvars;
   makeMat := X /. (Thread[vars -> #]) &;
   proj = makeMat /@ Orthogonalize@RandomReal[{-1, 1}, {n, m}];
   mat2 = 
    Total@MapThread[Times, {proj, dvars}, 1] + IdentityMatrix@Length@X;
   cons = And @@ (Thread[Eigenvalues[mat2] >= 0]);
   RegionPlot3D[cons, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, Mesh -> 5, 
    PlotStyle -> Opacity[.7], PlotPoints -> 5]
   );
Table[spectro2, {2}, {3}]

@IstvánZachar wikipedia has a somewhat scant definition of spectrahedron. But, it may be enough to go be. — rcollyer, Jan 26 '12 at 15:59

score 5 · Accepted Answer · answered Jan 26 '12 at 05:33

5

If the desire is to not have a surface appear when the region hits the boundary of the plot range, you could use something like:

Show[RegionPlot3D[Evaluate[cons], {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, 
  PlotRangePadding -> None, Mesh -> 5, PlotStyle -> Opacity[.7], 
  PlotPoints -> 10], PlotRange -> 2.9]

to truncate the plot range to an area inside the boundary.

enter image description here

answered Jan 26 '12 at 05:33

Brett Champion

20,779
2
64
121

Ah, clipping the output range...yes, seems to do what I needed – Yaroslav Bulatov Jan 26 '12 at 20:19

score 2 · Answer 2 · answered Jan 26 '12 at 06:02

For plotting 3D surfaces, there's ContourPlot3D. Here's an example from the documentation:

ContourPlot3D[x^3 + y^2 - z^2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

ContourPlot3D

However, I can't modify your code because no matter what I change it breaks, so this is all I can give you here. Could you clean it up a bit and document what it's doing so we can actually play around with it?

Visualizing 3×3 spectrahedra

2 Answers2

Linked