17

Why (-1.)^2. in Mathematica returns a complex number? It looks like in both C and Fortran it returns 1. Why does Mathematica behave differently than the other systems? Is it because the way Mathematica calculates the power is unique compared to others? If this is true then what are the advantages of this design?

I'm curious because it seems cost a "bug" in my code. Sometimes the code is more than 10X slower than other time, and it took me a while to figure out that the problem comes the following function

f[n_] := Compile[{{x, _Real}}, Cos[x]^n] 

f[2] /@ Range[0, 4 π, π/10]; // AbsoluteTiming
(* {0.000258, Null} *)

f[2.] /@ Range[0, 4 π, π/10]; // AbsoluteTiming
(* {0.140602, Null} *)

Notice that the second evaluation of f is much slower than the first, because cos[x]^2. is treated as a complex function and the uncompiled version is invoked.

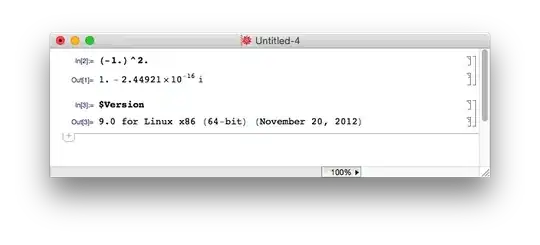
enter image description here

Here are some examples from other languages, it looks all of them gives 1 as the answer.

Fortran

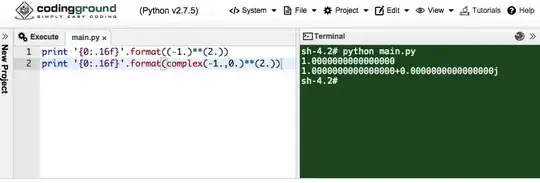
enter image description here

C

enter image description here

Python

enter image description here

Matlab/Octave

enter image description here

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
xslittlegrass
  • 27,549
  • 9
  • 97
  • 186
  • 2
    The imaginary components which are involved in the internal algorithms don't cancel exactly due to precision issues. Use Chop to remove the imaginary artifacts. – Bob Hanlon Jan 13 '15 at 22:52
  • 3
    Actually it's nor surprising. (-1)^2.1 and (-1)^1.9 do not have zero imaginary parts. Im[(-1)^x] == Sin[Pi x] crosses zero at x=2, but when using inexact numbers there's always a chance that we'd get a slight deviation from precise zero. It's just numerical error. Why C and Fortran don't do this? If you work with a data type that doesn't support imaginary numbers at all then you can't get imaginary results. pow(-1., 2.01) is nan in C. – Szabolcs Jan 13 '15 at 22:53
  • 2
    In other words this question is: why is Sin[2. Pi] not exact 0? You don't get exact 0 in C++ either – Szabolcs Jan 13 '15 at 22:54
  • Not sure how the internals work, but in general, a negative number to the power of a real number is a complex number, so this is probably just a manifestation of type-stability. As Mr. Wizard pointed out, a negative number to the power of an integer is always real-valued. – DumpsterDoofus Jan 13 '15 at 23:03
  • For a more visual explanation of why a complex output should be expected, note that $f(z)=(-1)^z$ maps the interval $[2-\epsilon,2+\epsilon]$ to a vertical stripe in the complex plane centered at 1. – DumpsterDoofus Jan 13 '15 at 23:42
  • 4
    A machine double, raised to a machine double power, will in effect compute exp(powlog(base)). `In[2]:= 2.Log[-1.]

    Out[2]= 0. + 6.28319 I

    In[3]:= Exp[%]

                       -16

    Out[3]= 1. - 2.44929 10 I

    `

     – Daniel Lichtblau Jan 13 '15 at 23:57
  • Compare to ev( (-1.)^(-2.)), bfloat; in maxima – Rolf Mertig Jan 14 '15 at 12:43
  • Look: Plot[{Re@#, Im@#} &@((-1)^x), {x, 1.5, 2.5}] – acl Jan 20 '15 at 21:27
  • @acl Thanks. I understand that the imaginary part is not zero when the x is not exactly 2. But I'm curious why Mathematica behaves different than the other systems? – xslittlegrass Jan 20 '15 at 21:30
  • 2
    @xslittlegrass the other systems follow IEEE754, which requires that they get the answer that they do. Mathematica doesn't. This still doesn't explain why Mathematica feels satisfied with 1.1 ULP error in this result; someone else will have to answer that one for you. – Oleksandr R. Jan 20 '15 at 21:45
  • FWIW, my 9.0.1.0 linux throws a "proceeding with uncompiled version" error on the real 2. – george2079 Jan 20 '15 at 22:03
  • Using Chop@Re@ in the compiled function fixes things without impacting performance much (I realize that's not really the point of the question though ) – george2079 Jan 20 '15 at 22:07
  • @xslittlegrass I see. No idea then. – acl Jan 20 '15 at 22:27
  • But why does '(-1)^2.' also return a microscopic complex component? Note that the '1' has no '.'. Only '(-1)^2' and '(-1.)^2' evaluate as one would expect. In fact there is no way to force this calculation to not return a complex component (CatchMachineUnderflow does nothing) except to put a Chop on top of it. – berniethejet Sep 05 '18 at 00:33

4 Answers4

9

My original answer (below) is wrong. Arbitrary precision does not fix this problem, I only fooled myself (and others) into thinking that it does. Now please consider:

Power[-1`5, 2`5]

1.0000 + 0.*10^-5 I

This agrees with the output of the effective computation that Daniel described in a comment:

power[base_, pow_] := Exp[pow*Log[base]]

power[-1`5, 2`5]

1.0000 + 0.*10^-5 I

Following that evaluation we get a complex value from Log when base is negative:

Log[-1`5]

0.*10^-5 + 3.1416 I

Given the method used complex numbers seem inherent in the calculation.

Mistaken assertion

Round-off errors occur in floating point calculations. You can use arbitrary precision to avoid these:

(-1`5)^2

1.0000
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • 5
    I think the question is really: why is Mathematica's Power function less accurate than those in other languages? Here we have 1.1 ULP of error. Practically speaking we can say that the other languages follow IEEE754 (which requires exact rounding, so <0.5 ULP error in all operations), and Mathematica doesn't. Some justification of this is probably called for so long as Mathematica gives inferior results. But, interestingly, we do not have these problems as soon as you go to arbitrary precision. – Oleksandr R. Jan 20 '15 at 21:49
  • @Oleksandr Thanks for the comment. By the way I believe I was mistaken regarding arbitrary precision and I revised my answer accordingly. – Mr.Wizard Jan 21 '15 at 02:11
  • 1
    +1 for Dan's comment explaining it (transcendental functions are not included in the IEEE754 specification, so >0.5 ULP error should be acceptable for them, even if technically the implementation of Power should not be done this way if we are following the standard), but I don't follow why arbitrary precision doesn't resolve the problem? SetPrecision[-1, $MachinePrecision]^SetPrecision[2, $MachinePrecision] gives an exactly rounded result; remove the $ and this is lost. The arbitrary-precision Log and Exp implementations seem more accurate than their machine-precision counterparts. – Oleksandr R. Jan 21 '15 at 10:22
  • N.B. result = SetPrecision[-1, $MachinePrecision]^SetPrecision[2, $MachinePrecision]; Log[2, 10^$MachinePrecision] - Log[2, 10^Accuracy@Im[result]] gives 3.05. But I don't know what to make of this; I am not sure if it is significance arithmetic telling us that we should have lost this much precision, or if we really have. – Oleksandr R. Jan 21 '15 at 10:32
6

My guess is that when you write 1. and 2. as opposed to 1 and 2 you are telling Mathematica that the numbers you are using are not integers but that they are rather real numbers whose best decimal representation is, as far as you know or within your accuracy criteria, 1.0 and 2.0. Thus, numerical methods are legitimate and you can expect numerical errors.

It is for a similar reason that1+1. returns 2. (a real) rather than 2 (integer).

Mathematica is aware of the issue as testified by this example:

Simplify[(-1.)^(2 z), Element[z, Integers]]
(* 1. *)
Simplify[(-1)^(2 z), Element[z, Integers]]
(* 1 *)
A.G.
  • 4,362
  • 13
  • 18
6

lets make a fair fortran test... raise a complex typed number 1 to the power:

   write(*,*)(-1.d0,0.d0)**2.,(-1.d0,0.d0)**2

(1.00000000000,-2.449212707...E-16 ) , ( 1.0000000000,0.000000000 )

also note in fortran the real power can not yield a complex result, that is (-1.)**.5 throws an error or yields NaN depending on the compiler so you see (-1.)**2. works only because (/if) the compiler is smart enough to recognize that 2. should be treated as an integer.

**the first test was with the gfortran compiler, intel fortran gives the expected

( 1.0000000000,0.000000000 ) , ( 1.0000000000,0.000000000 )

george2079
  • 38,913
  • 1
  • 43
  • 110
  • Which compiler/flags? – Oleksandr R. Jan 20 '15 at 22:30
  • no flags. See the edit though - the results may differ depending on how the compiler optimizes the code. – george2079 Jan 20 '15 at 22:39
  • Interesting. gcc is usually stricter about IEEE compliance than the Intel compiler, so to see this result is quite surprising. On the other hand, Intel has the better math library, so if this is a library call, it's not so surprising after all. – Oleksandr R. Jan 20 '15 at 22:56
0

(-1.)^2 does not return an imaginary number in Version 12.0; it returns 1.

CElliott
  • 560
  • 2
  • 7
  • 2
    I get an imaginary part: http://i.stack.imgur.com/F5UjW.png -- Note that the code to test is (-1.)^2., with a Real number 2., not an integer 2 as you have written. – Michael E2 May 12 '19 at 12:21
  • You can format inline code and code blocks by selecting the code and clicking the {} button above the edit window. The edit window help button ? is useful for learning how to format your questions and answers. You may also find this meta Q&A helpful – Michael E2 May 12 '19 at 12:23
  • The difference is in the inputs (integer exponent 2 vs real 2.0). – Daniel Lichtblau May 12 '19 at 20:08