Discretizing regions with pointy boundaries

Question

I'm trying to discretize a region with "pointy" boundaries to study dielectric breaking on electrodes with pointy surfaces. So far I've tried 3 types of boundaries, but the meshing functions stall indefinitely. I've let it run for several hours and it doesn't complete. Seems strange that it would take so long

ParametricPlot[{-Cos[u] (1.2 - Cos[(u - Pi)/2]^6) (0.2 + 
     Cos[10 u]^10), 
  Sin[u] (1.2 - Cos[(u - Pi)/2]^6) (0.2 + Cos[10 u]^10)}, {u, 0, 
  2 Pi}, PlotRange -> All]
ir = ParametricRegion[{{r Cos[u], r Sin[u]}, 
   0 <= u <= 2 Pi && 
    0 <= r <= (0.5 + 
       Cos[(u - (Pi/2))/2]^8 Cos[14 (u - (Pi/2))]^8)}, {r, u}]
ird = DiscretizeRegion[ir, MaxCellMeasure -> 0.02] (* never completes *)
Needs["NDSolve`FEM`"]
m = ToElementMesh[ir, 
  "BoundaryMeshGenerator" -> {"RegionPlot", "SamplePoints" -> 50}, 
  "MeshOrder" -> 1] (* never completes *)

Another attempt:

ParametricPlot[{ 
  Cos[u] Max[
    0.1, -Cos[u]] (1.2 - 
     Abs[Sin[10 Abs[((u - Pi))^(1/2)]]^(1/3)]), (1.2 - 
     Abs[Sin[10 Abs[((u - Pi))^(1/2)]]^(1/3)]) Sin[u] Max[
    0.1, -Cos[u]]}, {u, 0, 2 Pi}, PlotRange -> All]
ir2 = ParametricRegion[{{r Cos[u], r Sin[u]}, 
   0 <= u <= 2 Pi && 
    0 <= r <= 
     Max[0.1, -Cos[u]] (1.2 - 
        Abs[Sin[10 Abs[((u - Pi))^(1/2)]]^(1/3)])}, {r, u}]
m = ToElementMesh[ir2, 
  "BoundaryMeshGenerator" -> {"RegionPlot", "SamplePoints" -> 50}, 
  "MeshOrder" -> 1] (* never completes *)

Last attempt:

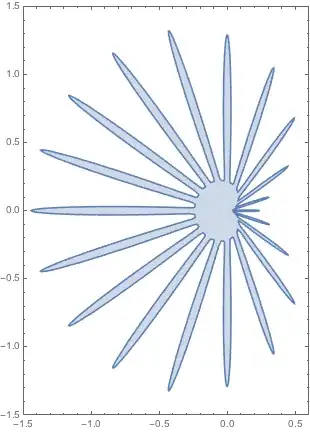
ParametricPlot[{-Cos[u] (1.2 - Cos[(u - Pi)/2]^6) (0.2 + 
     Cos[10 u]^10), 
  Sin[u] (1.2 - Cos[(u - Pi)/2]^6) (0.2 + Cos[10 u]^10)}, {u, 0, 
  2 Pi}, PlotRange -> All]
ir3 = ParametricRegion[{{r Cos[u], r Sin[u]}, 
   0 <= u <= 2 Pi && 
    0 <= r <= (1.2 - Cos[(u - Pi)/2]^6) (0.2 + Cos[10 u]^10)}, {r, u}]
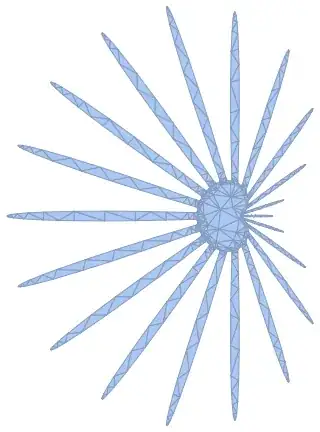
m = ToElementMesh[ir3, 
  "BoundaryMeshGenerator" -> {"RegionPlot", "SamplePoints" -> 50}, 
  "MeshOrder" -> 1] (* never completes *)

Answer 1

fn = {-Cos[u] (1.2 - Cos[(u - Pi)/2]^6) (0.2 + Cos[10 u]^10), 
   Sin[u] (1.2 - Cos[(u - Pi)/2]^6) (0.2 + Cos[10 u]^10)};
plot =
  ParametricPlot[fn, {u, 0, 2 Pi}, 
   PlotPoints -> Round[2 Pi (Sqrt@MaxValue[#.# &@D[fn, u],
          u])/0.2], PlotRange -> All];

Cases[plot, Line[p_] :> Polygon[p], Infinity] // 
  First // DiscretizeRegion

Or:

DiscretizeGraphics[Show[plot /. Line -> Polygon, PlotRange -> All]]

I get an error if I don't reset PlotRange. Perhaps a bug.

Answer 2

I would suggest not going through the Plot functions for this. They're designed to produce a good visual representation of the region, which is not necessarily the same as a good representation for doing numerical computation on. Besides, the plot already discretizes the region into a polygon, so the mesh refinement options of DiscretizeRegion or ToElementMesh cannot help to improve the accuracy of the boundary. It's best to maintain an analytical representation of the region right up until it goes into the mesh generation routine.

Unfortunately, Mathematica is not very good at dealing with ParametricRegions. (It can't even do

RegionPlot[
 ParametricRegion[{r Cos@t, r Sin@t}, {{r, 1, 2}, {t, 0, Pi/2}}], 
 PlotRange -> {{0, 2}, {0, 2}}]

correctly.) Your region can be easily expressed as an ImplicitRegion instead:

region = ImplicitRegion[
   With[{r = Sqrt[x^2 + y^2], u = ArcTan[-x, y]}, r <= f[u]], {x, y}];
RegionPlot[region, PlotRange -> {{-1.5, 0.6}, {-1.5, 1.5}}, AspectRatio -> Automatic]

(Mathematica also has a hard time figuring out the bounds of the region automatically, so sometimes you have to specify them manually.) Then DiscretizeRegion works fine:

DiscretizeRegion[region, {{-1.5, 0.6}, {-1.5, 1.5}}, 
 MaxCellMeasure -> 0.02, AccuracyGoal -> 3]

as does ToElementMesh:

Needs["NDSolve`FEM`"];
mesh = ToElementMesh[region, {{-1.5, 0.6}, {-1.5, 1.5}}, 
   "BoundaryMeshGenerator" -> "Continuation"];
Show[mesh["Wireframe"]]