Animate point going around a triangle

Question

How can I animate a point moving on a triangle's sides?
I can generate a triangle and point, but I have no idea how to define point movement. I'm guessing that I have to use $\sin$ and $\cos$ in coordinates, but I can't find a way to define the triangle in this way.
Can someone help me a bit with that?

point on triangle

score 22 · Accepted Answer · edited Jun 15 '15 at 14:12

22

If you interpret your geometric shape as a NURBS of degree 1 (linear), you can proceed with the following, extremely simple code:

pts = {{0, 0}, {1, 1}, {0.5, 1.5}}; (* just an example *)
s = BSplineFunction[pts, SplineClosed -> True, SplineDegree -> 1];
Animate[ParametricPlot[s[t], {t, 0, 1}, Epilog :> {Red, PointSize[Large], Point[s[t]]}], {t, 0., 1.}]

This yields the triangular (outer) graph of the following display:

Same BSplineFunction, but increased degree and custom weights

Just replace Animate by Manipulate to give the user control over the point.

Note This is a rather general approach applicable in wide areas, since you can vary your control points as well as the spline degree, but the BSplineFunction will always yield the curve between arguments 0 and 1. In essence, you can display quite every geometric shape using this approach. For more complex ones, some adjustment to B-spline weights will be necessary, though.

The inner of those curves result from the same control points as before, but degree 2 and weights explicitly given as SplineWeights -> {.1, 1, 1}. Just exchange the s-line above with this one:

s = BSplineFunction[pts, SplineClosed -> True, SplineDegree -> 2, SplineWeights -> {.1, 1, 1}];

I hope this might be of some help to you.

edited Jun 15 '15 at 14:12

J. M.'s missing motivation

124,525
11
401
574

answered Jan 24 '15 at 20:51

Jinxed

3,753
10
24

Simon, would you consider using a variation of your user name? We have a member of three years using the same name, and though he isn't as active recently it still confuses me when I see you post or comment. (This is merely a suggestion; you are not required to take action.) – Mr.Wizard Jan 25 '15 at 00:33
Simon might be a rather common user name, I take it.
Problem is: I had some problems with my Stackexchange account already, up to the point of having had to contact support for help... I will see what I can do, however, without messing up my account once again.

Did I mention, how inexplicably unintuitive the Stackexchange account management is? ;)
– Jinxed Jan 25 '15 at 01:14
@Mr.Wizard: I tried, but Stackexchange won't let me: I will have to wait until some time in February. Maybe you will have become acquainted to my user name until then. Either way: I can't change anything for the moment. :| – Jinxed Jan 25 '15 at 01:20
1

I second @Mr.Wizard because your contributions to the site are very well received. It wouldn't matter if you were the standard "novice new user type", but you aren't. And it's a lame to have that kind of confusion among two good site citizens. Please don't forget to try changing you user name once the site allows you. – Dr. belisarius Jan 25 '15 at 03:20
Simon, as a community elected moderator I believe I am able to change your user name. If you tell me what you would like I shall attempt it. – Mr.Wizard Jan 25 '15 at 03:45
Ah. Good to hear that. Please change the username to Jinxed. Thank you! – Jinxed Jan 25 '15 at 09:44
@Mr.Wizard: Please see my previous comment. I forgot to mention you explicitly. – Jinxed Jan 25 '15 at 13:17
@Jinxed Complete. – Mr.Wizard Jan 25 '15 at 19:43
@Mr.Wizard: Thanks! – Jinxed Jan 25 '15 at 20:17

DavidC · Answer 2 · 2015-02-17T02:55:20.810

Using `RegionNearest`

This approach should work regardless of whether the triangle is filled or not. Here, we will represent the triangle unfilled, i.e. as a one-dimensional region, r1, a line, embedded in a plane.

r1 = Line[{{0, 0}, {3, 1}, {2, 0}, {0, 0}}];
RegionDimension[r1]
RegionEmbeddingDimension[r1]

1
2

Get the radius of a circle, with the triangle centroid as center, that intersects the farthest vertex of the triangle.

c = RegionCentroid[r1];  (* the gray point *)
radius = Max[EuclideanDistance[c, #] & /@ {{0, 0}, {3, 1}, {2, 0}}];

Animate a black point going around the circle.

And display a (red) point on the triangle that is currently nearest to the black point on the circle.

Animator[Dynamic[n], {0, N[2 Pi], .01}]
Graphics[{r1, AbsolutePointSize[10],
  Gray, Point[c],
  Black, Dynamic@ Point[d = radius {Cos[n], Sin[n]} + c],
  {Red, Dynamic@Point[RegionNearest[r1, d]]},
  {Dashed, Circle[c, radius]}}]

animation2

Unusual in both method and result. +1 – Mr.Wizard Jan 25 '15 at 00:35 — Mr.Wizard, Jan 25 '15 at 00:35

score 13 · Answer 3 · edited Apr 13 '17 at 12:55

Thanks to kguler, I now know there is something like: LineScaledCoordinate.

vertices = Table[{Cos[i], Sin[i]}, {i, 0, 2 Pi, 2 Pi/3.}];
Needs["GraphUtilities`"]

Slider[Dynamic@t]
Graphics[{

  EdgeForm @ Thick, FaceForm @ None, Polygon @ vertices
  ,
  AbsolutePointSize @ 12, Red, Dynamic[Point[LineScaledCoordinate[vertices, t]]]
  }
 ]

Just in case you can't load GraphUtilities`, use Interpolation:

f = Interpolation[Table[{{i}, vertices[[i]]}, {i, Length@vertices}], 
                  InterpolationOrder -> 1]

Slider[Dynamic @ t, {1, 4}]
Graphics[{
        EdgeForm@Thick, FaceForm@None, Polygon@vertices
        , 
        AbsolutePointSize@12, Red, Dynamic[Point[f[t]]]
        }]

This method is different because each edge has parametric length of 1. If you want uniform "velocity" then you have to take care of {i} in Table.

Stelios · Answer 4 · 2015-01-25T15:42:48.403

11

e = {{0, 0}, {1, 1}, {5.5, 1.5}, {0, 0}}; (*triangle vertices*)

(*point position as a function of time*)
p[t_, e_] := Piecewise[{
    {(1 - t)*e[[1]] + t*e[[2]], 0 <= t <= 1},
    {(1 - (t - 1))*e[[2]] + (t - 1)*e[[3]], 1 < t <= 2},
    {(1 - (t - 2))*e[[3]] + (t - 2)*e[[1]], 2 < t <= 3}
    }];

(*animation*)
Animate[
 Show[
  Graphics[Line[e]],
  Graphics[{Red, PointSize[Large], Point[p[t, e]]}]
  ]
 , {t, 0, 3}
 ]

EDIT (Make the point move at constant speed)

Length of triangle edges:

d = EuclideanDistance[#[[1]], #[[2]]] & /@ Partition[e, 2, 1]

Modified p function so that the point moves at a normalized speed of d[[1]] (i.e., move along the first edge in time equal to $1$)

pver2[t_, e_] := Piecewise[{
    {(1 - t)*e[[1]] + t*e[[2]], 0 <= t <= 1},

    {(1 - (t - 1)/(d[[2]]/d[[1]]))*e[[2]] + (t - 1)*
       e[[3]]/(d[[2]]/d[[1]]), 1 < t <= 1 + d[[2]]/d[[1]]},

    {(1 - (t - (1 + d[[2]]/d[[1]]))/(d[[3]]/d[[1]]))*
       e[[3]] + (t - (1 + d[[2]]/d[[1]]))*e[[1]]/(d[[3]]/d[[1]]), 
     1 + d[[2]]/d[[1]] < t <= 1 + d[[2]]/d[[1]] + d[[3]]/d[[1]]}}];

Animation:

Animate[Show[Graphics[Line[e]], 
  Graphics[{Red, PointSize[Large], Point[pver2[t, e]]}]], {t, 0, 
  1 + d[[2]]/d[[1]] + d[[3]]/d[[1]]}]

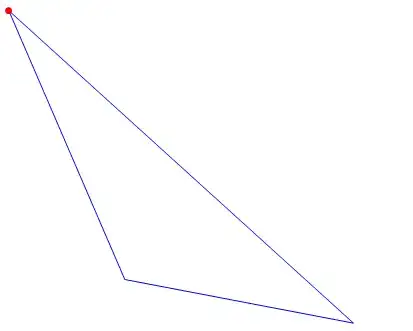
enter image description here

edited Jan 25 '15 at 15:42

answered Jan 24 '15 at 18:23

Stelios

1,381
1
11
16

1

Should e be modified to {{0, 0}, {1, 1}, {0.5, 1.5}, {0, 0}} to close the triangle? – bbgodfrey Jan 24 '15 at 18:49
@bbgodfrey Indeed, thanks for noticing – Stelios Jan 24 '15 at 18:50
Very simple and clean solution. Is't there a way to make a point move in same speed on all sides? I know that I can adjust t param to slow it down or make it move faster, but it will still change speed on sides. – Dcortez Jan 25 '15 at 13:14
@Dcortez Please see edited answer for an (probably not elegant) implementation of the constant speed animation – Stelios Jan 25 '15 at 15:28
Maybe not cleanest but working. Thank you very much for help. – Dcortez Jan 25 '15 at 15:46

score 4 · Answer 5 · answered Aug 26 '19 at 11:46

Manipulate[
 Graphics[{
   Line[p[[{1, 2, 3, 1}]]],
   PointSize@Large, Red,
   Point[With[{f = Floor[i], t = FractionalPart[i]}, {1 - t, t}.p[[Mod[{f, f + 1}, 3, 1]]]]]
   }],
 {{p, {{0, 0}, {0.8, 0.9}, {0.5, 1.5}}}, Locator}, {i, 1, 4}]

It's also easy to generalize to polygons.

kglr · Answer 6 · 2019-08-26T19:26:10.610

SeedRandom[77]
coords = Append[#, First@#] &@RandomReal[1, {3, 2}];

`Arrowheads` + `Clock`

Dynamic[Graphics[{Arrowheads[{{.05, Clock[{0, 1}, 5, 3]}}], 
   Blue, Arrow @ coords}, Axes -> False]]

With a custom arrowhead:

pnt = Graphics[{Red, PointSize[Large], Point[{0, 0}]}]; 

Dynamic[Graphics[{Arrowheads[{{.05, Clock[{0, 1}, 5, 3], pnt}}], 
   Blue, Arrow @ coords}, Axes -> False]]

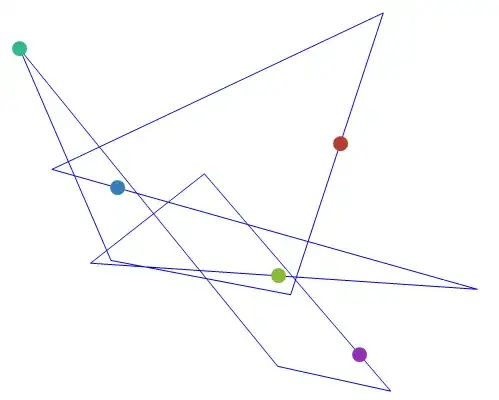
Multiple points moving at different speeds on the boundary of an arbitrary polygon and stopping after three tours:

SeedRandom[77]
coords = Append[#, First@#] &@RandomReal[1, {10, 2}];
pnts = Table[Graphics[{ColorData[63, "ColorList"][[i]], AbsolutePointSize[15], 
     Point[{0, 0}]}], {i, 5}];

Dynamic[Graphics[{Blue, 
   Arrowheads[Table[{.05, Mod[i/5 + Clock[{0, 1}, i, 3], 1], pnts[[i]]}, {i, 1, 
      5}]], 
   Arrow @ coords}, Axes -> False, PlotRange -> {{-.1, 1.1}, {-.1, 1.1}}]]

`Arrowheads` + `Animate`

Animate[Graphics[{Arrowheads[{{.05, t, pnt}}], Blue, Arrow @ coords}, 
  Axes -> False], {t, 0, 1}]

score 4 · Answer 7 · edited Apr 13 '17 at 12:19

Here is my modest attempt, based on a formula given in this math.SE answer, with a few affine transformations thrown in:

triangle[pts_?MatrixQ, t_] :=
         AffineTransform[{Transpose[{{2, -1, -1}/3, {0, 1, -1}/Sqrt[3]}.pts], Mean[pts]}][
               Sec[t - π (2 Floor[3 t/(2 π)] + 1)/3] {Cos[t], Sin[t]}/2]

pts = {{0, 0}, {1, 1}, {1, 3}/2};
mt[t_] = triangle[pts, t];
tpic = ParametricPlot[mt[t], {t, 0, 2 π}, Frame -> True];

Animate[Show[tpic, 
             Epilog -> {{Directive[ColorData[1, 1], AbsolutePointSize[4]], Point[pts]},
                        {Directive[Red, AbsolutePointSize[8]], Point[mt[u]]}}],
        {u, 0, 2 π, π/12}]

point going around a triangle

Animate point going around a triangle

7 Answers7

Using `RegionNearest`

`Arrowheads` + `Clock`

`Arrowheads` + `Animate`

Linked

Animate point going around a triangle

7 Answers7

Using RegionNearest

Arrowheads + Clock

Arrowheads + Animate

Linked

Using `RegionNearest`

`Arrowheads` + `Clock`

`Arrowheads` + `Animate`