No legends in parametric plot

Question

plotting some descibing functions, I wondered why I don't get any legends in my plot.

The describing functions (and options):

N1[a_] := (4 d)/(π a)
N2[a_] := (4 d)/π 1/(I ϵ + Sqrt[a^2 - ϵ^2])
N3[a_] := (4 d)/(π a) Sqrt[1 - (ϵ/a)^2] - I (4 d ϵ)/(π a^2)
N4[a_] := (4 d)/(π a) E^(-I ArcSin[ϵ/a])

opt = {d -> 1, ϵ -> 5}

and the ParametricPlot

ParametricPlot[{
   (*{Re@N1[a],Im@N1[a]},*)
   {Re[N2[a]], Im[N2[a]]},
   {Re@N3[a], Im@N3[a]},
   {Re@N4[a], Im@N4[a]}
   } /. opt, {a, .001, 1000},
 PlotRange -> All,
 PlotPoints -> 1000,
 MaxRecursion -> 15,
 PlotLegends -> "Expressions"]

(The first function is out commented, because it has wired behavior. Bonus for the one who can explain it ;-) )

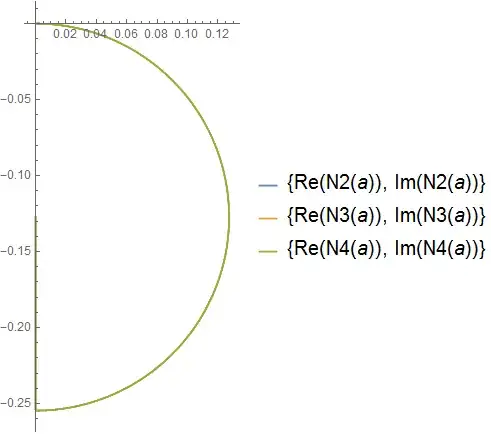
What I get is this:

enter image description here

Why are there no legends? Is it because of the userdefined functions?

@Nasser According to Mr. Wizard's answer the problem behind your link doesn't last for Mma V10!? — Phab, Jan 29 '15 at 08:04

score 6 · Accepted Answer · edited Apr 13 '17 at 12:55

This is a variation of Plot draws list of curves in same color when not using Evaluate. By using /. the head of the first argument is ReplaceAll rather than a List, and the styling subroutine of ParametricPlot does not know what to do with it.

Make the substitutions part of the definitions and you get this:

N1[a_] := (4 d)/(π a)                                       /. opt
N2[a_] := (4 d)/π 1/(I ϵ + Sqrt[a^2 - ϵ^2])                 /. opt
N3[a_] := (4 d)/(π a) Sqrt[1 - (ϵ/a)^2] - I (4 d ϵ)/(π a^2) /. opt
N4[a_] := (4 d)/(π a) E^(-I ArcSin[ϵ/a])                    /. opt

opt = {d -> 1, ϵ -> 5}

ParametricPlot[
 {{Re@N2[a], Im@N2[a]},
  {Re@N3[a], Im@N3[a]},
  {Re@N4[a], Im@N4[a]}}, {a, .001, 1000}, PlotRange -> All, PlotPoints -> 1000, 
 MaxRecursion -> 15, PlotLegends -> "Expressions"]

enter image description here

+1 for the link to the topic with an explanation why it doesn't work. — Phab, Jan 29 '15 at 08:02

No legends in parametric plot

1 Answers1

Linked