Well, over-pursuing similarity of Mathematica code and traditional math notation does more harm than good, still, it's possible to create a nabla operator in Mathematica, here's my approach:
(*$PrePrint=.*)
$PrePrint = # /.
Derivative[id__][f_][args__] :>
TraditionalForm[
HoldForm@D[f[args], ##] &[
Sequence @@ (DeleteCases[Transpose[{{args}, {id}}], {_, 0}] /. {x_, 1} :> x)]] &;
Clear[$independentVariable, ▽, Δ]
$independentVariable = {x, y, z};
▽ /: ▽ f_ := Grad[f, $independentVariable]
▽·f_ := Div[f, $independentVariable]
▽ /: ▽\[Cross]f_ := Curl[f, $independentVariable]
▽·▽ := Δ
▽ /: ▽^2 := Δ
Δ /: Δ f_ := Laplacian[f, $independentVariable]
CenterDot /: (v_·▽) f_ := Grad[f, $independentVariable].v
CenterDot /: (m_?MatrixQ·▽)\[Cross]f_ :=
TensorContract[LeviCivitaTensor[3].D[f, {$independentVariable}].m\[Transpose], {2, 3}]
Usage:
▽ f[x, y, z]
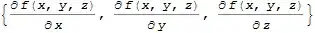
▽·{f[x, y, z], g[x, y, z], h[x, y, z]}

▽\[Cross]{f[x, y, z], g[x, y, z], h[x, y, z]}

▽·▽ f[x, y, z]
▽^2 f[x, y, z]
Δ f[x, y, z]
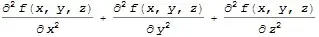
({Subscript[v, x], Subscript[v, y], Subscript[v, z]}·▽) f[x, y, z]

({Subscript[v, x], Subscript[v, y], Subscript[v, z]}·▽){f[x, y, z], g[x, y, z],h[x, y, z]}

Alst = Array[Subscript[A, ##] &, {3, 3}];
vector = #[x, y, z] & /@ {u, v, w};
test1 = (Alst·▽)\[Cross]vector

Notice the · is \[CenterDot], and ▽ is \[EmptyDownTriangle] rather than \[Del].
To type ▽ easier, try the technique in this and this post.
Not sure if the solution will fail in more complicated cases.
BTW the $PrePrint function is modified from the code here.

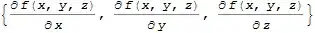


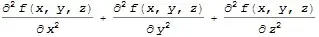






TimesandPowerwith these interpretations. Better use clearly distinct notation to make code easier to understand. – Jens Mar 05 '15 at 17:24GradandLaplacian, and relatedDivandCurl. These symbols have new input forms quite close to what you're asking for. – kirma Mar 05 '15 at 19:51Gradfunction insteadGrad[vector1.vector2, {x, y, z}]which gives{Subscript[b, x] Subscript^(0,1)(a,x)+Subscript[a, x] Subscript^(0,1)(b,x),Subscript[b, y] Subscript^(0,1)(a,y)+Subscript[a, y] Subscript^(0,1)(b,y),Subscript[b, z] Subscript^(0,1)(a,z)+Subscript[a, z] Subscript^(0,1)(b,z)}What are the superscript referring to? – Physkid Mar 09 '17 at 13:41Derivative[1,0][f]in StandardForm. – Szabolcs Mar 09 '17 at 13:45HoldForm[Curl[v, {x, y, z}]]and see how it formats. This is different from interpreting that form when you enter it. Traditional notation is ambiguous. When you are talking to a computer you want to be clear and unambiguous. – Szabolcs Mar 09 '17 at 14:08