Strange extrapolation in ListContourPlot?

Question

I have some Table of {x,y,z} values (energy as a function of radial and azimuthal frequencies in a galaxy if you care to know):

dat = Import["https://dl.dropboxusercontent.com/u/659996/odd-data.m"];

If I plot the position of the {x,y}

pl1 = Most /@ Flatten[dat, 1] // ListPlot

I get this

Mathematica graphics

Note that there is nothing pathological in the distribution of points as seen from this 3D view

Map[{Hue[#[[3]]], Point[#]} &, Flatten[dat, 1]] // Graphics3D

Mathematica graphics

If I now plot contours of z[x,y], I get that:

pl2 = ListContourPlot[Flatten[dat, 1], PlotLegends -> Automatic,PlotRange -> All]

Mathematica graphics

PROBLEM

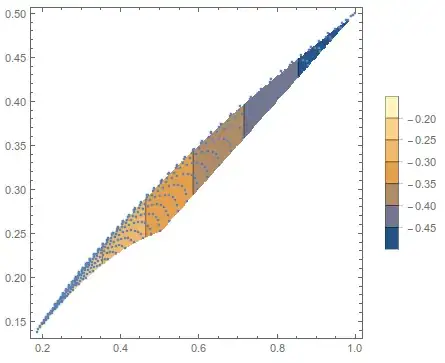
Now the puzzling fact is that it seems Mathematica gives me contours at values of {x,y} which I have not sampled. This is best seen in the superposition:

Show[pl2, pl1]

Mathematica graphics

e.g. for values of x=0.3 y=0.175.

QUESTION

Is this a bug?

or am I missing something obvious?

UPDATE

I guess Mathematica cannot guess any obvious boundary to my sets of x,y coordinates other than the Convex Hull has mentioned by @belisarius so the Bug is in my head.

@belisarius indeed it does but you find it makes sense to extrapolate on the convex hull? — chris, Feb 03 '15 at 17:08
Looks like the correct partition of the space based on $z$ values, which needn't conform to the sampling of the (x,y) space, any more than the elevation of a mountain range must conform to the sampling of latitude and longitude. — David G. Stork, Feb 03 '15 at 17:08

score 6 · Accepted Answer · edited Apr 13 '17 at 12:55

It is possible to restrict the plotting region by using RegionFunction. However, it is also necessary to construct a concave hull of the data, and use a higher MaxPlotPoints when making the contour plot. Using RunnyKine's code from here to construct the region,

dat = Flatten[
   Import["https://dl.dropboxusercontent.com/u/659996/odd-data.m"], 1];
reg = alphaShapes2D[DeleteDuplicates@dat[[All, ;; 2]], .33];
RegionPlot[reg]

We can now get the proper contour plot,

Show[
 ListContourPlot[dat, PlotLegends -> Automatic, PlotRange -> All, 
  RegionFunction -> Function[{x, y, z}, RegionMember[reg, {x, y}]], 
  MaxPlotPoints -> 100],
 ListPlot@dat[[All, ;; 2]]
 ]

Strange extrapolation in ListContourPlot?

1 Answers1

Linked

Related