1

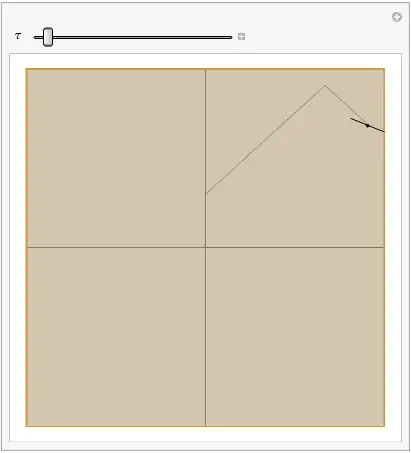
Simulate a polygon bouncing with collision detection inside a circle/polygon.

the example can be see in help page by searching WhenEvent;

ball2d[r_?NumericQ] := Reap@NDSolveValue[{{x'[t] == vx[t], y'[t] == vy[t], x1'[t] == vx[t],

y1'[t] == vy[t]}, WhenEvent[{x[t]^2 + y[t]^2 == 1,   x1[t]^2 + y1[t]^2 == .9}, {x1[t] ->


x[t] + (pp = RandomReal[.1]),   y1[t] -> y[t] + Sqrt[0.02 - pp^2], vy[t] -> -.9 vy[t],


vx[t] -> -.9 vx[t]}],x[0] == 0, y[0] == 0, x1[0] == .1, y1[0] == .1, vx[0] == 1,


vy[0] == 1}, {x[t], y[t], x1[t], y1[t]}, {t, 0, 200},DiscreteVariables -> {vx, vy}];


{sol1, v} = ball2d[4/3];


Manipulate[ ParametricPlot[#, {t, 0, [Tau]}, Frame -> True, PlotRange -> 2,


PlotPoints -> 10, PlotStyle -> Thickness[0.02],Epilog -> {PointSize[.05], Point[# /. (t -> [Tau])], 




ContourPlot[{x^2 + y^2 == 1}, {x, -1, 1}, {y, -1, 1}][[1]]}] & /@


Partition[sol1, 2], {{[Tau], 11.9}, 0.01, 198},  SaveDefinitions -> True]

The following example show a stick bouncing inside a circle, not so good

What's the right way?

How can I go forward to replace the stick with a triangle or a polygon? and futher a polygon3d?

Any examples?

Manipulate[ ParametricPlot[#, {t, 0, [Tau]}, Frame -> True, PlotRange -> 2,

PlotPoints -> 10, PlotStyle -> Thickness[0.0001],Epilog -> {Pink, Thick, 




Line[{{#[[1]], #[[2]]}, {#[[3]], #[[4]]}}] /. (t -> [Tau]),  ContourPlot[{x^2 + y^2 == 1}, {x, -1, 1}, {y, -1, 1}][[1]]}] &@


sol1, {{[Tau], 0.01}, 0.01, 198, .1}, SaveDefinitions -> True]

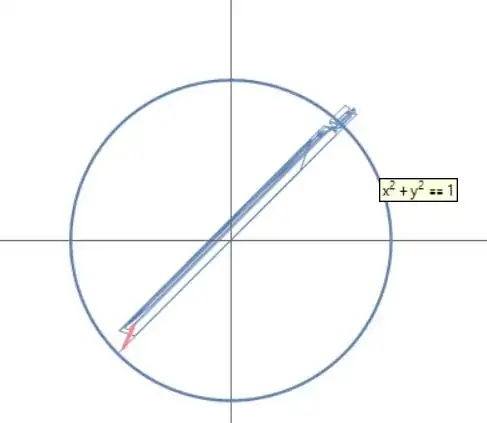
enter image description here

The reference posted by Mr.Wizard is about a point model which is much simpler. My question is about extending the example in WhenEvent help page. However the animation is really shown by that example, can you image a stick bouncing like that?

Community
  • 1
HyperGroups
  • 8,619
  • 1
  • 26
  • 63

1 Answers1

2

The keypoint is the equation and the events. The example in a rotation line, the keypoint is to express endpoints of a line.

p = 1;
ball2d[r_?NumericQ] := Reap@NDSolveValue[{
 x'[t] == vx[t],
 WhenEvent[{Abs[(x[t] + 0.1*Cos[p*t])] - 1 >= 0, 
   Abs[(x[t] - 0.1*Cos[p*t])] - 1 >= 0},
  If[x[t] >= 0, vx[t] -> -Abs@vx[t], vx[t] -> Abs@vx[t]]
  ],
 y'[t] == vy[t],
 WhenEvent[{Abs[(y[t] + 0.1*Sin[p*t])] - 1 >= 0, 
   Abs[(y[t] - 0.1*Sin[p*t])] - 1 >= 0}, 
  If[y[t] >= 0, vy[t] -> -Abs@vy[t], vy[t] -> Abs@vy[t]]
  ],
 x[0] == 0, y[0] == 0.3, vx[0] == 0.1 + RandomReal[0.1], 
 vy[0] == 0.1 + RandomReal[0.1]
 }, {x[t], y[t], vx[t], vy[t]}, {t, 0, 200, .01}, 
DiscreteVariables -> {vx, vy}];
{sol1, flag} = ball2d[.01]
g = Manipulate[
 ParametricPlot[#, {t, 0, \[Tau]}, Frame -> True, FrameTicks -> None,
  PlotRange -> 1, Axes -> True, PlotPoints -> 500, 
 PlotStyle -> Thickness[0.000], 
 Epilog -> {RegionPlot[{-1 < x < 1, -1 < y < 1}, {x, -1, 
      1}, {y, -1, 1}][[1]], PointSize[.01], 
   Point[# /. (t -> \[Tau])], 
   Line[{# - 0.1 {Cos[t], Sin[t]}, # + 
       0.1 {Cos[t], Sin[t]}} /. (t -> \[Tau])]}] &@
   sol1[[1 ;; 2]], {{\[Tau], 5.9}, 0.01, 200, .01}, 
  SaveDefinitions -> True]

Debug

endpoint1[x_,y_,q_]:={x+0.1*Cos[q],y+0.1*Sin[q]}
endpoint2[x_,y_,q_]:={x-0.1*Cos[q],y-0.1*Sin[q]}
debug[t0_]:=Block[{},
x1=sol1[[1]]/.t->t0;
y1=sol1[[2]]/.t->t0;
vx1=sol1[[3]]/.t->t0;
vy1=sol1[[4]]/.t->t0;
{x1, y1, vx1, vy1, endpoint1[x1,y1,t0], endpoint2[x1,y1,t0]}
]

There is a problem, when vy[0]=0.05[a little small], event check will fail in some values. One can use my raw debug method to see. For example, when vy[61.1] is not set to be -0.01.

debug[60.8]
{-0.52062,0.908,-0.1,0.01,{-0.565109,0.818442},{-0.47613,0.997558}}
debug[61.1]
{-0.55062,0.911,-0.1,0.01,{-0.566656,0.812294},{-0.534583,1.00971}}

enter image description here

HyperGroups
  • 8,619
  • 1
  • 26
  • 63