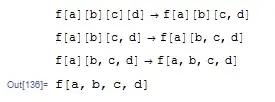How to visualize pattern matching process?

Question

I want a function that does the same job like ReplaceRepeated, and can make the matching process visible.

I searched the Internet but didn't find any existing code or package that meets my requirement, so I tried to write one:

Clear[myReplaceRepeated];
myReplaceRepeated[lis_List, rule_, n_: Infinity] := 
Module[{variables, mat = rule[[1]], data, tem}, 
variables = 
ToExpression@
StringCases[
 ToString[mat], (vars : WordCharacter ..) ~~ "_" | "__" | "___" :> vars];
If[variables != {},

testQ = Table[Cases[#1, #2 -> i, {0}], {i, variables}] &;
data = 
Reap[FixedPointList[(Sow[testQ[#, mat]]; # /. rule) &, lis, 
   n]][[2, 1]]; 
Labeled[Grid[Prepend[data, variables], Frame -> All, 
 Background -> {Lighter /@ 
    Hue /@ Range[0, 1, 1/Length[variables]]}], 
Column[{lis, "the rule is", rule}], Top],

Labeled[
Grid[tem = Most@FixedPointList[# /. rule &, lis, n], Frame -> All,
  Background -> {None, {Lighter /@ 
     Hue /@ Range[0, 1, 1/Length[tem]]}}], 
Column[{lis, "the rule is", rule}], Top]
]]

It works in some cases:

Example 1

myReplaceRepeated[{1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 8}, 
{Longest[a___], b_, c__, b_, d___} -> {b, b, a, c, d}]

enter image description here

Example 2

myReplaceRepeated[{1, a, 2, b, 3, c}, _?NumericQ -> F[Infinity], 4](*4 is set the MaxIterations*)

From "Mathematica Cookbook"

Example 3

myReplaceRepeated[{1, 2}, {a_, b_} -> {{a}, {b}}, 5]](*5 is also set the MaxIterations*)

From "Mathematica Cookbook"

but fails in some other cases:

myReplaceRepeated[f[a][b][c][d], g_[x_][y__] -> g[x, y]]
myReplaceRepeated[Log[Sqrt[a (b c^d)^e]], {Log[x_ y_] :> Log[x] + Log[y], Log[x_^k_] :> k Log[x]}]

How to improve my myReplaceRepeated?

Is there really no existing tool for the visualization of pattern matching?

Edit:

Let me explain my function with the following example.

lis = {1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 8};
rule = {Longest[a___], b_, c__, b_, d___} -> {b, b, a, c, d};
mat(*short for match*) = rule[[1]];

I want to know how those variables i.e. a,b,c and d in rule match the sub-sequence in lis when lis //. rule executes.

To monitor how those variables match, I need to first know what variables rule contain:

variables = 
ToExpression@StringCases[
ToString[mat], (vars : WordCharacter ..) ~~ "_" | "__" | "___" :> vars]

{a, b, c, b, d}

Then I find out how these variables match lis respectively, for example the following piece of code shows a matches 1, 3, 1, 4 in lis.

Notice the level is {0}, otherwise we get {}

Cases[{1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 
8}, {Longest[a___], b_, c__, b_, d___} -> a, {0}]

{1, 3, 1, 4}

These are combined in a loop.

Table[Cases[{1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 
8}, {Longest[a___], b_, c__, b_, d___} -> i, {0}], {i, variables}]

{{1, 3, 1, 4}, {1}, {3, 4, 2, 7}, {1}, {8}}

The output means a represents {1, 3, 1, 4},b represents {1}, c represents {3, 4, 2, 7}, the next b represents the latter {1} and d represents {8} in lis.

Then I define a testQ to combine all these together:

testQ = Module[{variables}, 
variables = 
 ToExpression@
  StringCases[
   ToString[#2], (vars : WordCharacter ..) ~~ 
     "_" | "__" | "___" :> vars];
Table[Cases[#1, #2 -> i, {0}], {i, variables}]] &;
testQ[lis, mat]

{{1, 3, 1, 4}, {1}, {3, 4, 2, 7}, {1}, {8}}

The functionality of ReplaceRepeated is achieved by FixedPointList:

 data = Reap[
 FixedPointList[(Sow[
   testQ[#, 
    mat]]; # /. {Longest[a___], b_, c__, b_, d___} -> {b, b, a, c,
      d}) &, {1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 8}]][[2, 1]];
 Grid@data

This is almost the output of example 1, except for the coloring.

You may noticed that the variables in the above code can't be {}, so a rule like

  lis = {1, a, 2, b, 3, c}; rule = _?NumericQ -> F[Infinity]; 
  variables = 
  ToExpression@
  StringCases[
  ToString[mat], (vars : WordCharacter ..) ~~ "_" | "__" | "___" :> vars]

{}

will cause problem, that's why I add a If in myReplaceRepeated.

So long my code gets the ability to handle example 1 ~ 3, but if lis and rule are:

lis = f[a][b][c][d]; rule = g_[x_][y__] -> g[x, y]; mat = rule[[1]]; 
variables = 
ToExpression@
StringCases[
ToString[mat], (vars : WordCharacter ..) ~~ "_" | "__" | "___" :> 
vars]!={}

True

My program fails, how to fix it?

It's an interesting question, but I don't quite understand the rule of the colorization. Could you explain it more please? — Silvia, Feb 10 '15 at 08:32
I tried to improve the expressions of your question. (Wish I didn't make it worse… ) Well, To be honest, personally I feel your Edit a little verbose… — xzczd, Feb 11 '15 at 03:48
@xzczd Thank you indeed. Your English is better than mine. SE is really have a typeset than Baidu tieba sites. — partida, Feb 11 '15 at 05:08

xzczd · Accepted Answer · 2015-02-10T16:38:35.000

There exists a simple trick for your purpose, here is my implementation:

f[a][b][c][d] //. g_[x_][y__] :> g[x, y] /; (Print[g[x][y] -> g[x, y]]; True)

enter image description here

Log[Sqrt[a (b c^d)^e]] //.
 {Log[x_ y_] :> Log[x] + Log[y] /; (Print[Log[x y] -> Log[x] + Log[y]]; True),
  Log[x_^k_] :> k Log[x] /; (Print[Log[x^k] -> k Log[x]]; True)}

enter image description here

Not as colorful as yours, but you can use the trick therein as the core of your myReplaceRepeated.

Update

Here's my trial for a general function monitoring pattern-matching. Needless to say, achieving a perfectly general monitoring function is hard and I'm sure (Yeah, sure) my function will fail under more complicated situations, but it at least works for your samples.

ClearAll[show]
SetAttributes[show, HoldAll]
show[f_] := 
 Module[{i = 1}, 
  Quiet[ReleaseHold[
    Hold[f] /. 
      (Except[MaxIterations, a_] -> b_) :> a :> Evaluate[b] /. 
      (a_ :> b_) :> 
        a :> b /; (Print[(a /. Longest | Shortest | Repeated | RepeatedNull -> List /. 
                     Pattern :> 
                       Composition[Evaluate, Sequence @@ # &, 
                         With[{color = ColorData[1][i++]}, (Style[#, color] &) /@ #] &, 
                         Most, List]) -> b]; 
                  True)], 
  RuleDelayed::rhs]]

This function is (naively) attempted to handle all the code involving pattern-matching that explicitly containing Rule or RuleDelayed. Let's try it.

Example 1:

show[{1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 8} //. 
       {Longest[a___], b_, c__, b_, d___} :> {b, b, a, c, d}]

enter image description here

Here the scope of different patterns are marked by different colors, and the scope of Longest is additionally marked by {}.

Example 2:

show@ReplaceRepeated[{1, a, 2, b}, _?NumericQ -> F[Infinity], MaxIterations -> 2]

enter image description here

~~To relieve the embarrassment I cut down the size of this example,~~ I admit that for this example the visual effect of your myReplaceRepeated beats my show, but show does monitor the matching process.

Example 3:

show@ReplaceRepeated[{1, 2}, {a_, b_} -> {{a}, {b}}, MaxIterations -> 5]

enter image description here

Notice in this and the previous example the Except[MaxIterations, a_] part in the definition of show plays a role. If you want to make this function more general, more exceptions should be included in this part. (Or maybe I should think out a completely new testing method?)

Example 4:

show[f[a][b][c][d] //. g_[x_][y__] -> g[x, y]]

enter image description here

Notice that in this example the Evaluate inside Composition is necessary or the Sequence won't disappear.

Example 5:

show[Log[Sqrt[a (b c^d)^e]] //. {Log[x_ y_] :> Log[x] + Log[y], Log[x_^k_] :> k Log[x]}]

enter image description here

This example is actually the simplest among the 5.

As mentioned above, the show function is still quite incomplete, but you can use it as a start. I may also improve it later, but now I'd like to go to bed :)

You may want to look into using Reap and Sow instead of Print if you want full control of the outputted rules. — Greg Hurst, Feb 10 '15 at 15:25
@ChipHurst I understand what you mean.If I use Sow and Reap and combine his method,my solution can be shorter — partida, Feb 10 '15 at 15:44
@ChipHurst Yeah, Reap and Sow is undoubtedly a better choice. The initial intention of this answer is only to show that trick so I chose the relatively simpler Print to avoid distraction :) — xzczd, Feb 10 '15 at 16:21
@user15961 You don't need to accept that quick, feel free to wait for 24 hours or more so your question may attract better answers. — xzczd, Feb 11 '15 at 02:08
Regarding evaluation you might find interest in my mkMatchRules function posted in answer to the question linked in the comment below this question. You already have my vote of course. — Mr.Wizard, Feb 11 '15 at 08:28

How to visualize pattern matching process?

1 Answers1

Linked