Suppose I wanted to use Mathematica graphics primitives to create a gradient of colors between two circular arcs. It's easy enough to make an area between two circles a solid color, but what if I wanted to have the area between two colors blur from black to white as you go out in radius?
VertexColor provides this kind of functionality for polygons, but I'm not sure how it would work for shapes containing circular arcs.
I just realized that the parametrization in my previous revision of this answer is a special case of bipolar coordinates. Every rectangle in bipolar coordinates $\theta_1<\theta<\theta_2,\ \tau_1<\tau<\tau_2$ is a region between four arcs. Two arcs is just a simple special case.
Here is my realization of bipolar coordinates with special stretching to make texture more uniform and avoid shrinking at points $\tau=\pm\infty$. This parametrization have two additional parameters $(\theta_0,\tau_0)$. It is a reference point where texture is locally uniform.
bc[{τ1_, τ2_, τ0_: 1}, {θ1_, θ2_, θ0_: Scaled[0.5]}, opts___] :=
Module[{u, v, t, q, t1, t2, q1, q2, μ, ν},
μ = Abs@Tan[θ0/2] /. Scaled@x_ :> Rescale[x, {0, 1}, {θ1, θ2}] // Chop;
ν = Abs@Tanh[τ0/2] /. Scaled@x_ :> Rescale[x, {0, 1}, {τ1, τ2}] // Chop;
{t1, t2} = Which[μ == 0, #, Chop[1/μ] == 0, -1/#, True, ArcTan[# μ]] &@Tanh[{τ1, τ2}/2];
{q1, q2} = If[ν == 0, Tan[#/2], ArcTan[ν+1 - Cos@#(ν-1), Sin@#(ν-1)] + #/2] & /@ {θ1, θ2};
u = Which[μ == 0, t, Chop[1/μ] == 0, -1/t, True, Tan@t/μ];
v = If[ν == 0, q, Tan@q/ν];
First@Cases[#, _GraphicsComplex, ∞] &@
ParametricPlot[{u (1 + v^2), (1 - u^2) v}/(1 + u^2 v^2), {t, t1, t2}, {q, q1, q2}, opts]]
You can use any option of the parametric plot
Graphics[bc[{0.5, 4}, {-π, π/2}, Mesh -> Full, PlotStyle -> {Opacity[1],
Texture@LinearGradientImage[{Red, Yellow, Blue}]}, BoundaryStyle -> Black]]
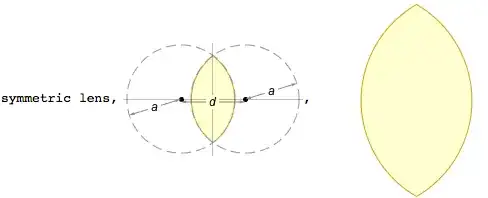
As mentioned above, two arcs is a special case
arcs[p1_, r1_, p2_, r2_, opts___] :=
Module[{α = ArcTan @@ (p1 - p2), d = Norm[p2 - p1], a, τ1, τ2, d2},
d2 = (d^2 + r1^2 - r2^2)/(2 d); a = Sqrt[d2^2 - r1^2];
τ1 = Log[-(d2 + a)/r1]; τ2 = Log[(d2 + a - d)/r2];
GeometricTransformation[#2, {Abs@a {{Cos@α, -Sin@α}, {Sin@α,
Cos@α}}, #}] &[p2 - {Cos@α, Sin@α} a Coth[τ2],
If[Im@a == 0, bc[{τ1, τ2}, {0, 2 π, π/2}, opts], α += π/2;
bc[{-∞, ∞}, {Im@τ1, Im@τ2}, opts]]]
]
p1 = {0.6, 0.2};
p2 = {0.9, 0.6};
r1 = 0.5;
r2 = 0.7;
Graphics[arcs[p1, -r1, p2, r2, PlotStyle -> {Opacity[1],
Texture@LinearGradientImage[{Top, Bottom} -> {Red, Yellow,
Blue}]}, BoundaryStyle -> Black]]
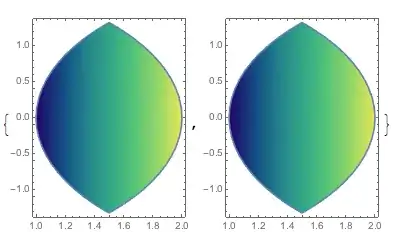
The output region (intersection, complement or union) depends on signs of radii
Graphics[arcs[p1, r1, p2, r2, PlotStyle -> {Opacity[1],
Texture@LinearGradientImage[{Top, Bottom} -> {Red, Yellow,
Blue}]}, BoundaryStyle -> Black]]
In the current realization the intersection of initial circles is not necessary
p1 = {2.5, 0.2};
p2 = {0.9, 0.6};
r1 = -3.5;
r2 = 0.7;
Graphics[{arcs[p1, r1, p2, r2, PlotStyle -> {Opacity[1],
Texture@LinearGradientImage[{Red, Yellow, Blue}]},
BoundaryStyle -> Black]}]
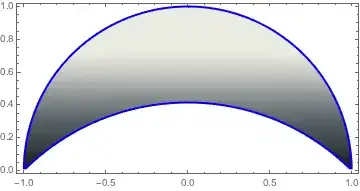
You can do even open regions (here RegionFunction limits the region)
p1 = {0.5, 0.2};
p2 = {-1.1, 0.6};
r1 = -0.5;
r2 = -0.7;
Graphics[arcs[p1, r1, p2, r2, Mesh -> Full, PlotStyle -> {Opacity[1],
Texture@LinearGradientImage[{Red, Yellow, Blue}]},
BoundaryStyle -> Black, RegionFunction -> Function[{x, y}, x^2 + y^2 < 200],
MaxRecursion -> 3], PlotRange -> 4]
It is not possible to do this directly circular arcs. VertexColor works for triangles (any other polygon will be broken up into triangles before the colours are applied). If you need a gradient fill for an arbitrary shape, it needs to be approximated using a set of triangles first, then each triangle coloured individually. There are several ways to do this, for example:
DensityPlot[x, {x, -1, 1}, {y, -1, 1},
RegionFunction -> Function[{x, y}, (x - .5)^2 + y^2 < 1 && (x + .5)^2 + y^2 < 1]]
Add the Mesh -> All option to actually see the triangles it generates:
LaminaDataLaminaData is a good place to start.
This leads to two approaches, each of which ultimately displays the figure in RegionPlot.
Approach 1 is based on graphics objects (the intersection region of two disks). The graphics object then employs BoundaryDiscretizeRegion or DiscretizeRegion, the former being more efficient for not tracking points within the region.
Approach 2 uses a formula associated with an ImplicitRegion. This turns out to be very similar to Szabolcs' approach. I didn't generate the formula on my own but obtained it directly from LaminaData[].
I wasn't sure how to draw the figure so I searched around in LaminaData[] and stumbled across the symmetric lens). Here are it's diagram and image. The Diagram revealed that it was the intersection of two disks.
LaminaData[Entity["Lamina", "LensSymmetric"], #] & /@ {"Name", "Diagram", "Image"}
The Region property described the region as the intersection of two disks.
The ImplicitRegion property gave a formula. These give rise to two different approaches, described below.
LaminaData[Entity["Lamina", "LensSymmetric"], "Region"]
LaminaData[Entity["Lamina", "LensSymmetric"], "ImplicitRegion"]
r = RegionIntersection[Disk[{0, 0}, 2], Disk[{3, 0}, 2]];
dr = DiscretizeRegion[r];
bdr = BoundaryDiscretizeRegion[r];
RegionPlot[#, ColorFunction -> "BlueGreenYellow", AspectRatio -> Full] & /@ {dr, bdr}
It was a straightforward matter to insert parameters into the formula. Formal d and formal a were set to 1. They can be tweaked as desired. Formal x and formal y were replaced with x, y.
The color function was then applied.
d = 1; a = 1;
r = ImplicitRegion[y^2 + (x - d/2)^2 <= a^2 && y^2 + (x + d/2)^2 <= a^2, {x, y}];
RegionPlot[r, ColorFunction -> "BlueGreenYellow", AspectRatio -> Full]
Not sure if I understand your question correctly, but here is my approach:
With[{r = 1},
RegionPlot[
x^2 + y^2 < r^2 && x^2 + (y + r)^2 > 2 r^2, {x, -1, 1}, {y, 0, 1},
MaxRecursion -> 5, AspectRatio -> Automatic,
ColorFunction -> (Blend[{White, Black}, #] &)]]
Or using ColorFunction and ColorData:
With[{r = 1},
RegionPlot[
x^2 + y^2 < r^2 && x^2 + (y + r)^2 > 2 r^2, {x, -1, 1}, {y, 0, 1},
MaxRecursion -> 5, AspectRatio -> Automatic,
ColorFunction -> Function[{x, y}, ColorData["GrayTones"][y .99]],
BoundaryStyle -> Directive[Red, Thick]]]
The available Gradients you can find with the command ColorData["Gradients"]:
{AlpineColors,Aquamarine,ArmyColors,AtlanticColors,AuroraColors,AvocadoColors,BeachColors,BlueGreenYellow,BrassTones,BrightBands,BrownCyanTones,CandyColors,CherryTones,CMYKColors,CoffeeTones,DarkBands,DarkRainbow,DarkTerrain,DeepSeaColors,FallColors,FruitPunchColors,FuchsiaTones,GrayTones,GrayYellowTones,GreenBrownTerrain,GreenPinkTones,IslandColors,LakeColors,LightTemperatureMap,LightTerrain,MintColors,NeonColors,Pastel,PearlColors,PigeonTones,PlumColors,Rainbow,RedBlueTones,RedGreenSplit,RoseColors,RustTones,SandyTerrain,SiennaTones,SolarColors,SouthwestColors,StarryNightColors,SunsetColors,TemperatureMap,ThermometerColors,ValentineTones,WatermelonColors}
You can also "steer" the gradient:
With[{r = 1},
RegionPlot[
x^2 + y^2 < r^2 && x^2 + (y + r)^2 > 2 r^2, {x, -1, 1}, {y, 0, 1},
MaxRecursion -> 5, AspectRatio -> Automatic,
ColorFunction ->
Function[{x, y}, ColorData["GrayTones"][y Sqrt[2]]],
BoundaryStyle -> Directive[Blue, Thick]]]
