I am processing MRP data, with BOM relations as pairs of part number strings. I want to construct lists that represent the linear graphs defined by these pairs.
Here is some code to generate random sample data, with real-world distribution of lengths of linear graphs:
SeedRandom[1234];
chainLengths = Round /@ RandomVariate[ParetoDistribution[2., 8.], 300];
chainStrings = RandomSample[DictionaryLookup["s" ~~ ___], Total[chainLengths]];
chains = Block[
{cs = chainStrings},
Reap[
Do[
Sow[cs[[\;\;c]]]; (*remove backslashes, triggers unwanted formatting*)
cs=cs[[c+1;;]];
Null,
{c, chainLengths}
]
][[2, 1]]
];
chainStrings === Flatten[chains]
Out[]= True
Histogram[Length /@ chains]
chainParts = Reap[
Do[
Sow[#[[1]] -> #[[2]]] & /@ Partition[c, 2, 1],
{c, chains}
]
][[2, 1]];
chainParts = RandomSample[chainParts, Length[chainParts]];
And here is my code to construct the linear graph lists from the pair data (fail-fast sanity assertions commented out):
buildChains = Block[
{a, f, p, currentPass, nextPass, fatalError0,},
(*fatalError0::fatalReport="buildChains fatalError0: `1`";
fatalError0[msg_]:=(
Message[fatalError0::fatalReport,ToString[msg]];
Abort[]
);*)
a = {#} & /@ Complement[
First /@ chainParts, Last /@ chainParts];
currentPass = chainParts;
nextPass = {};
While[Length[currentPass] >= 1,
Do[
f = r[[1]];
p = Position[a, {___, f}];
If[p === {}, AppendTo[nextPass, r]; Continue[]];
(*If[{Length[p],Depth[p],LeafCount[p]}=!={1,3,3},
fatalError0[{"{Length[p],Depth[p],LeafCount[p]}=!={1,3,3}",p}]
];*)
p = p[[1, 1]];
a[[p]] = Append[a[[p]], r[[2]]],
{r, currentPass}
];
(*If[currentPass===nextPass,
Print[a];
Print[nextPass];
fatalError0[{"currentPass===nextPass",a,nextPass}]
];*)
currentPass = nextPass;
nextPass = {}
];
a
];
Sort[chains] === Sort[buildChains]
Out[]= True
Is there a simpler way to do this with MMA graph functionality? Or more efficient/elegant MMA code, regardless? I imagine the complexity is poor using Position for a linear search.
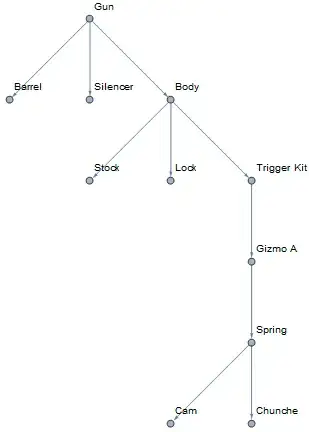
Graph[chainParts]? – Mr.Wizard Feb 20 '15 at 20:51