7

I saw a couple of posts dicretizing the graphic and generate DelaunayMesh to get volume of 3D object. The issue I'm having is that DelaunayMesh creates a bigger solid covering the original one, resulting more volume. Please see the following.

Let's say I have this 3D solid defined as below. In spherical coordinate,

R[θ_, ϕ_] := Abs[Cos[θ]]^2

or in Cartesian system

pf[θ_, ϕ_] := {Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]}*R[θ, ϕ];

This object has two lobes as shown below.

plot = ParametricPlot3D[pf[θ, ϕ], {θ, 0, π}, {ϕ, 0, 2 π}]

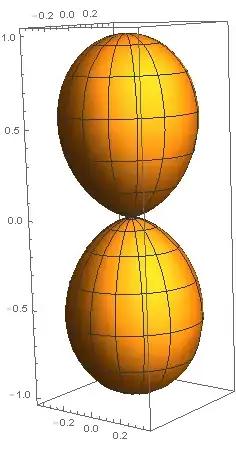
enter image description here

where its volume from spherical integral is 0.598399,

NIntegrate[ρ^2 Sin[θ], {θ, 0, π}, {ϕ, 0, 2 π}, {ρ, 0, R[θ, ϕ]}]

After discretizing 

displot = DiscretizeGraphics[Normal[plot /. (Lighting -> _) :> Lighting -> Automatic]]

I get

enter image description here

which still has two lobes, but with DelaunayMesh the feature disappears

hull = DelaunayMesh[MeshCoordinates[displot]]

enter image description here

And now it has different volume of 0.784115, greater than 0.598399 from the direct integration.

Volume[hull]

So I would like to know the best way to create mesh which gives the volume as precise as possible, both from a symbolic expression R(theta,phi) or from sampled points {{1,1,1},{3,2,2},....}.

One of the object I'm dealing with looks like this. Has many lobes, no symmetry.enter image description here

Here are more examples of distortion when I generate DelaunayMesh from a graphic.

From Parametricplot3D,

enter image description here

Then DelaunayMesh gives

enter image description here

Xnei
  • 73
  • 6
  • Sorry, maybe there's something I'm missing, but why can't you just keep using your NIntegrate[ρ^2 Sin[θ], ...] method? –  Feb 25 '15 at 08:04
  • If I had analytic expression for ρ, then I would do so. However I rather have discretized data points, basically a list of {ρ,θ,ϕ} coordinates. That's why I couldn't keep using NIntegrate. – Xnei Feb 25 '15 at 15:48
  • How did you generate the last plot? –  Feb 25 '15 at 16:57
  • It is from ParametricPlot3D[pf//.sol[θ,ϕ] {θ, 0, π}, {ϕ, 0, 2 π}], where sol[θ,ϕ] is a solution from numerically solving differential equations. I can draw it from manually sampled points. In this case, I think interpolation is automatically done by Mathematica. However, distortion occurs when you convert the graphic to DelaunayMesh. – Xnei Feb 25 '15 at 18:28

2 Answers2

7

DiscretizeGraphics already hands out a MeshRegion, so you could go along these lines:

meshonly = 
  With[{coords = MeshCoordinates[displot]}, 
    MeshCells[displot, 1] (* 0: points, 1: lines, 2: faces ... *) /. 
    Line[{a_, b_}] :> Line[{coords[[a]], coords[[b]]}]]

Graphics3D@meshonly

lines from MeshRegion extracted and displayed

This will also work for your the more exotic shape you displayed.

Volume

The volume can be calculated by calculating the volume of each tetraeder constructed from the mesh triangle with some fixed (for all calculations!) fourth point. The volume is either added or subtracted from the total volume, depending on the direction of the surface normal, which is given by the vertex ordering in Mathematica's output already, so you can go about this issue in the following way:

Total@With[{coords = MeshCoordinates[displot]}, 
   MeshCells[displot, 2] /. 
    Polygon[{a_, b_, c_}] :> 
     coords[[a]].Cross[coords[[b]], coords[[c]]]]/6
(* .585457 *)

The final divisor is required, since actually six volumes are calculated by the above operation.

The difference between the original result Mathematica provides and this one might be the effect of DiscreteGraphics.

It is possible to extract the actual polygons from the original plot, also, but one finds multi-vertex-polygons there (I did not check, if they are planar or convex or self-intersection-free), which require triangularization themselves, which is not all that difficult, but requires checking mentioned conditions and dealing with the situations encountered on a case-by-case-basis first, which I did not.

Nevertheless, I hope you can make some use of my answer!

Further reference: this publication

Jinxed
  • 3,753
  • 10
  • 24
  • You can get a huge improvement out of this by applying Compile. I.e. creating a compiled function, say compiledDotCross, which simply takes the place of coords[[a]].Cross[coords[[b]], coords[[c]]]] and then applying this. For me that dropped computation time by over 20 times on a class of regions I use frequently. In fact, it rivals the built-in Volume when you do this. – b3m2a1 Jan 05 '17 at 22:28
3

Are you sure NIntegrate won't work?

ρ[θ_?NumericQ,ϕ_?NumericQ] := sol[θ,ϕ]
SphericalPlot3D[ρ[θ,ϕ], {θ, 0, π}, {ϕ, 0, 2 π}]
NIntegrate[ρ[θ,ϕ]^3/3 Sin[θ], {θ, 0, π}, {ϕ, 0, 2 π}]

Assuming that sol[θ,ϕ] returns the value of your function.

2012rcampion
  • 7,851
  • 25
  • 44