Computing the equivalence classes of the symmetric transitive closure of a relation

Question

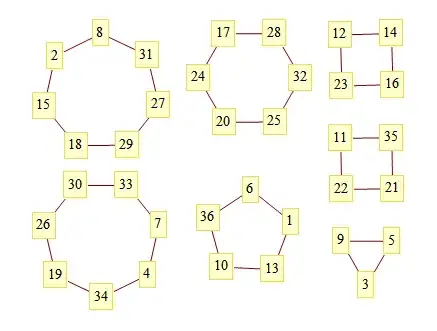
I have a list of pairs, for example:

pairs={{13, 10}, {12, 14}, {10, 36}, {35, 11}, {3, 5}, {1, 6},
{20, 24}, {21, 22}, {33, 7}, {31, 8}, {31, 27}, {32, 25}, 
{21, 35}, {34, 19}, {18, 15}, {14, 16}, {9, 5}, {4, 7}, 
{1, 13}, {15, 2}, {6, 36}, {4, 34}, {8, 2}, {9, 3}, {25, 20},
{19, 26}, {22, 11}, {23, 12}, {32, 28}, {30, 33}, {23, 16},
{24, 17}, {29, 27}, {26, 30}, {17, 28}, {18, 29}};

pairs can be seen as the definition of a relation $R$. $x$ and $y$ satisfy the relation if and only if {x,y} $\in$ pairs. I need to compute the equivalence classes of the symmetric transitive closure of $R$.

In other words, I need to compute a list eqvclss. The elements of eqvclss are lists themselves. For example, 13, 10, 36, 6, 1, ... should all be in the same list in eqvclss. (If you understand that, then I explained the question properly; if you don't, say so in the comments so I can try to improve).

From {13,10} and {10, 36}, you conclude that 10 and 13 belong together. But 13 also belongs with 1 because {1, 13} exists. However, there is no pair {1, 10} or {10, 1}, so 1 shouldn't be in the same group as 10, which is in the same group as 13 which belongs with 1. So the problem for Gather is that your identity relation is not transitive. As a result, you have to give up some conditions. Maybe you want all gathered groups to be numbers that are at least indirectly connected? — Jens, Jun 29 '12 at 05:29
@Jens Thanks for your comment. I see now. I did some drastic edits to the question (prior to seeing your comment). Now it's more to the point of what I want. Your comment now seems out of context, but it does answer the original question. — a06e, Jun 29 '12 at 05:32

kglr · Accepted Answer · 2018-01-26T16:03:00.363

12

ConnectedComponents

Using Daniel Lichtblau's answer to a related question

ConnectedComponents[pairs] //Sort /@ # & //Sort (* thanks: CarlWoll *)

{{3, 5, 9},
{11, 21, 22, 35},
{12, 14, 16, 23},
{1, 6, 10, 13, 36},
{17, 20, 24, 25, 28, 32},
{2, 8, 15, 18, 27, 29, 31},
{4, 7, 19, 26, 30, 33, 34}}

In versions prior to 10.3 use

 ConnectedComponents[Graph[UndirectedEdge @@@ pairs]] //Sort /@ # & //Sort

MatrixPower

Implementing transitive closure using MatrixPower:

m = Max@pairs;

(*the adjacency matrix of atomic elements in pairs:*)
SparseArray[pairs ~Append~ {i_, i_} -> 1, {m, m}];

(*symmetrize the adjacency matrix:*)
% + %\[Transpose] // Sign;

(*find the transitive closure:*)
Sign @ MatrixPower[N@%, m];

(*eliminate duplicate rows,and extract the atomic elements of pairs in each row:*)
Select[DeleteDuplicates @ Normal @ %, Tr@# > 1 &];
Join @@ Position[#, 1] & /@ %;

(*organize:*)
Sort[Sort /@ %]

{{3, 5, 9},
{11, 21, 22, 35},
{12, 14, 16, 23},
{1, 6, 10, 13, 36},
{17, 20, 24, 25, 28, 32},
{2, 8, 15, 18, 27, 29, 31},
{4, 7, 19, 26, 30, 33, 34}}

edited Jan 26 '18 at 16:03

answered Jun 29 '12 at 05:34

kglr

394,356
18
477
896

+1 I think like this better than my answer. – a06e Jun 29 '12 at 05:43
@becko, thanks for the vote. (Does the edit answer your request re horizontal scrollbar?) – kglr Jun 29 '12 at 06:05
Yes. The annoying scrollbar is gone. Thanks. – a06e Jun 29 '12 at 06:11
Slightly simpler is ConnectedComponents[pairs] – Carl Woll Jan 26 '18 at 15:54
Thank you @Carl. Updated with the simpler version. – kglr Jan 26 '18 at 16:03

score 6 · Answer 2 · edited Apr 13 '17 at 12:55

6

Adapting Heike's fine answer from the prior question:

pairs //. x_ :> Union @@@ Gather[x, # ⋂ #2 =!= {} &]

{{1, 6, 10, 13, 36},
 {12, 14, 16, 23},
 {11, 21, 22, 35},
 {3, 5,  9},
 {17, 20, 24, 25, 28, 32},
 {4, 7, 19, 26, 30, 33, 34},
 {2, 8, 15, 18, 27, 29, 31}}

edited Apr 13 '17 at 12:55

Community

1

answered Jun 29 '12 at 05:57

Mr.Wizard

271,378
34
587
1,371

I had not seen that. I can see is almost the same to what I did. – a06e Jun 29 '12 at 06:01
@becko and I did not see your answer before posting this, nevertheless I think it is different enough to be of interest. Do you agree? – Mr.Wizard Jun 29 '12 at 06:05
Yes. Besides, your way is more elegantly coded. – a06e Jun 29 '12 at 06:10

score 5 · Answer 3 · answered Jun 29 '12 at 05:39

Here's code for version 7:

Needs["Combinatorica`"]

gr = FromUnorderedPairs @ pairs;

ConnectedComponents @ gr

{{1, 6, 10, 13, 36},
 {2, 8, 15, 18, 27, 29, 31},
 {3, 5, 9},
 {4, 7, 19, 26, 30, 33, 34},
 {11, 21, 22, 35},
 {12, 14, 16, 23},
 {17, 20, 24, 25, 28, 32}}

GraphPlot[gr, VertexLabeling -> True]

Mathematica graphics

score 4 · Answer 4 · edited Apr 13 '17 at 12:55

I have separately posted this method as an answer to this question

If you want to preserve the order in which the vertices are connected within each cycle,

ExtractCycles (in the Combinatorica package) may also be of interest.

For example

Needs["Combinatorica`"]
ExtractCycles@FromUnorderedPairs@pairs

gives

(* { {28, 17, 24, 20, 25, 32, 28},

{23, 12, 14, 16, 23},

{35, 11, 22, 21, 35},

{34, 4, 7, 33, 30, 26, 19, 34},

{9, 3, 5, 9},

{15, 2, 8, 31, 27, 29, 18, 15},

{13, 1, 6, 36, 10, 13} } *)

score 2 · Answer 5 · answered Jun 29 '12 at 05:34

I just found a way to do it:

SymmetricTransitiveClosure[pairs : {{_, _} ..}] := 
    FixedPoint[DeleteDuplicates /@ 
        Flatten /@ Gather[#, Intersection[#1, #2] =!= {} &] &, pairs]

I won't acccept this yet. Perhaps someone comes up with something better.

Computing the equivalence classes of the symmetric transitive closure of a relation

5 Answers5

ConnectedComponents

MatrixPower

Linked

Related