How do I pad numbers to the left so that all are the same length?

Question

I have a list of numbers like

{-6, 1, 3, 23}

and want to get a list of strings, all of the same length, with zeros padding on the left as needed, like

{"-6", "01", "03", "23"}

The closest I can get following the documentation is with something like

NumberForm[{-6, 1, 3, 23}, 1, NumberPadding -> {"0", ""}]

which (astonishingly) produces

{"-6", "01", "03", "023"}

How I can simply get my strings to all be the same length, padded as needed with zeros?

What do you desire for the first entry: "-06" or "0-6" or "-006"? — David G. Stork, Mar 03 '15 at 18:24
Oh... it was unclear whether you wanted all strings to have the length 3 (in this case)... as in "023". Let me work on this.... — David G. Stork, Mar 03 '15 at 18:29
@raxacoricofallapatorius Do you want every and all strings to be of length 2 in every case (not just in your example)? You never want to apply the transformation to numbers such as 123 or -11? — David G. Stork, Mar 03 '15 at 18:46
@DavidG.Stork: Just like the example. Never more than one digit negative numbers and never more than two digit positives. — orome, Mar 03 '15 at 18:51

score 13 · Accepted Answer · answered Apr 04 '15 at 14:29

13

As of 10.1 this is built in to Mathematica with StringPadLeft:

StringPadLeft[#,2,"0"]&@*ToString/@{-6,1,3,23}

{"-6", "01", "03", "23"}

answered Apr 04 '15 at 14:29

orome

12,819
3
52
100

Could you please elucidate on the meaning of &@*? – Oscillon Sep 15 '19 at 01:41
2

@Oscillon Composition – orome Sep 15 '19 at 01:46

kglr · Answer 2 · 2015-03-03T20:46:58.997

6

ClearAll[nF]
nF = With[{l = #, p = #2}, NumberForm[l, p, SignPadding -> True, NumberPadding -> {"0", ""}, 
         NumberFormat -> (StringTake[#1, -(p + 1)] &)]] &;

nF[{-6, 1, 3, 23}, 1]
(* {-6, 01, 03, 23} *)

nF[{-6, 1, 3, 23, 123}, 2]
(* {-06, 001, 003, 023, 123} *)

Note: You can also use PaddedForm instead of NumberForm.

edited Mar 03 '15 at 20:46

answered Mar 03 '15 at 20:38

kglr

394,356
18
477
896

score 4 · Answer 3 · answered Mar 03 '15 at 18:57

4

Taking under consideration your assumptions:

StringTake["0" <> ToString[#], -2] & /@ {-6, 1, 3, 23}

answered Mar 03 '15 at 18:57

Kuba

136,707
13
279
740

Sean · Answer 4 · 2021-05-29T20:23:35.737

Here is an answer that is loosely based upon kglr's previous answer. The below solution has been generalized to also handle decimal numbers and scientific form. Your example number list only contained small integers, but others who find this post may find the generalization useful.

The code:

AltNumberFormat[n_, f___, 
  opts : OptionsPattern[{NumberForm, "AltPadding" -> ""}]] := With[{
   IsExtraPad = 
    MatchQ@First[OptionValue@NumberPadding /. Automatic -> {""}],
   altPad = OptionValue@"AltPadding"
   },
  NumberForm[
   N@n, f, FilterRules[{opts}, Options@NumberForm],
   NumberFormat -> Function[{m, b, e}, With[
      {s = 
        StringReplace[m, StartOfString ~~ _?IsExtraPad -> altPad]},
      If[e == "", s, Row[{s, b^e}, "\[Times]"]]
      ]]]]

Usage is exactly the same as regular NumberForm, with the addition of an extra AltPadding option. This would usually be used if you wanted to pad with leading zeros (without the extra zeros!) but still get your numbers to left-align, by padding positive numbers with leading spaces.

Test cases:

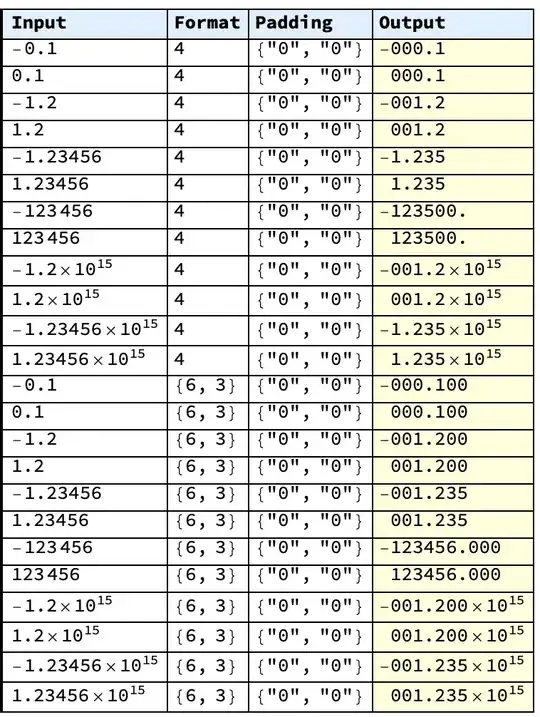
hdr = Prepend[
   Item[#, BaseStyle -> Bold, Background -> LightBlue] & /@ {"Input", 
     "Format", "Padding", "Output"}];
Row@Map[Grid[hdr@#, Frame -> All, Alignment -> Left, 
       Background -> {{4 -> LightYellow}}] &]@
    Transpose@Flatten[#, 2] &@
 Table[
  {mn, f, Style[p, ShowStringCharacters -> True], 
   AltNumberFormat[mn, f, NumberPadding -> p, SignPadding -> True, 
    AltPadding -> " "]},
  {f, {Unevaluated@Sequence[], 4, {6, 3}}},
  {n, {0.1, 1.2, 1.23456, 123456, 1.210^15, 1.2345610^15}},
  {m, {-1, 1}},
  {p, {Automatic, {"", "0"}, {"0", "0"}}}
  ]

Output:

C. E. · Answer 5 · 2015-03-03T18:59:48.563

2

One way:

If[StringLength@# == 1, "0" <> #, #] &@*ToString /@ {-6, 1, 3, 23}

Another way:

StringJoin@*(ToString /@ PadLeft[#, 2] &)@*Characters@*ToString /@ {-6, 1, 3, 23}

edited Mar 03 '15 at 18:59

answered Mar 03 '15 at 18:36

C. E.

70,533
6
140
264

So there's no built-in way to do this? Any idea what the reasoning behind the way NumberForm works could possibly be? I really don't understand the philosophy behind the Mathematica language design (c.f.: [str(n).zfill(2) for n in numbers]). – orome Mar 03 '15 at 18:42
@raxacoricofallapatorius Take a look at the newest solution. There is a built in function, but in order to use it we must first convert our string into a list. – C. E. Mar 03 '15 at 18:52
So the second solution is incomplete. – orome Mar 03 '15 at 18:58
@raxacoricofallapatorius Argh, I forgot to convert it back into a string. Now it's less elegant; I'd go with the first option. I'd go with it anyway because it's easy to understand; if you look at it in 6 months you will still know what it does. – C. E. Mar 03 '15 at 19:00
Thanks. That works. I'm still puzzled what (if any) design philosophy could have lead to this sort of thing. [str(n).zfill(2) for n in numbers] is not only something I'll understand in 6 months, but something that I can remember to recreate in 6 months (or years). – orome Mar 03 '15 at 19:05
Whats the "@*"? New in 10 I suppose? Anyway another way to write basically the same thing: StringJoin @@ PadLeft[Characters@ToString@#, 2, "0"] & /@ {-6, 1, 3, 23} – george2079 Mar 03 '15 at 20:59
@raxacoricofallapatorius In some languages strings are simply arrays of characters. In this case it makes sense to handle padding of both strings and arrays with the same function. Strings in Mathematica is not implemented as a list, in fact strings are "atomic". I can only speculate that this has something to do with it. – C. E. Mar 03 '15 at 22:13
@george2079 Nice version, I forgot about the third argument of PadLeft. It's just a shorthand for Composition. – C. E. Mar 03 '15 at 22:13
I had the same problem and I don't understand why PaddedForm[5, 2, NumberPadding -> {"0", ""}] gives 005, PaddedForm[15, 2, NumberPadding -> {"0", ""}] gives 015 and then surprisingly: PaddedForm[125, 2, NumberPadding -> {"0", ""}] gives 0125. Thanks for the solutions anyway! – Santiago Mar 19 '15 at 10:31

george2079 · Answer 6 · 2015-03-04T13:48:42.060

2

just for fun..we can define a zfill function

 zfill[n_, f_String: "0"] := 
      Function[{s}, 
        StringJoin[ConstantArray[f, Max[0, n - StringLength[s]]], s]];

then the operation is quite similar to your python expression:

 zfill[2] /@ ToString /@ {-6, 1, 3, 23}

{"-6", "01", "03", "23"}

edited Mar 04 '15 at 13:48

answered Mar 03 '15 at 21:12

george2079

38,913
1
43
110

I find this a good one! – Santiago Mar 19 '15 at 10:32

score 0 · Answer 7 · answered May 29 '21 at 20:34

0

Using sprintf that I describe in this answer, you can do Map[sprintf["%02i", #] &, {-6, 1, 3, 23}] to get {"-6", "01", "03", "23"}.

answered May 29 '21 at 20:34

evanb

6,026
18
30

How do I pad numbers to the left so that all are the same length?

7 Answers7

Linked