To extend the other answers, if you're going to be using the derivative of Abs often in your computations and do not need the complex absolute value, then you can define the Derivative of Abs once and for all, using whichever formula for the derivative of Abs you find convenient.
Derivative[1][Abs][x_] = Piecewise[{{1, x > 0}, {-1, x < 0}}, Indeterminate];
Plot[Evaluate@D[Abs[x], x], {x, -10, 10}, Exclusions -> {0}]

Note that one must use Evaluate on the derivative. (see, for instance, General::ivar is not a valid variable when plotting - what actually causes this and how to avoid it?).
To Unset the definition, do the following:
Derivative[1][Abs][x_] =.
You can also localize the definition of the derivative to a block of code as follows:
Internal`InheritedBlock[{Derivative},
Derivative[1][Abs][x_] = Piecewise[{{1, x > 0}, {-1, x < 0}}, Indeterminate];
...
<code>
...
]
The definition of Derivative is automatically reset in this case.



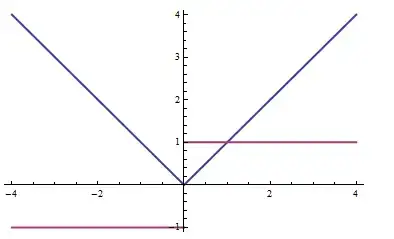

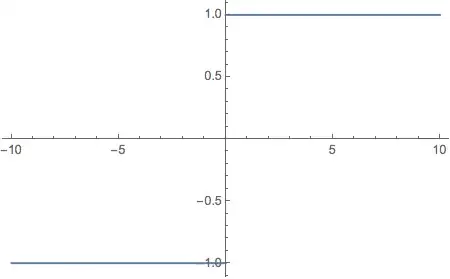
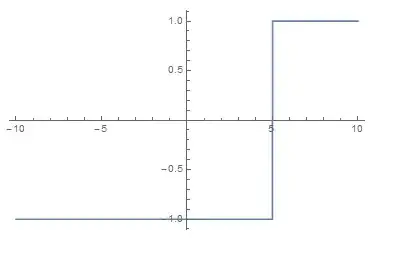
Plot[x/Abs[x], {x, -10, 10}]– Nasser Mar 08 '15 at 11:29