2

I am trying to generate a poincare map for a system whose reduced energy manifold looks like the following surface.

(x/a)^2 +(y/b)^2 +(z/c)^2=1

I want to find a lot of sample points(initial conditions) on the above mentioned ellipsoid.

Can anyone suggest a nice elegant way of doing this?

So far I have tried the following

a1[y_] := R Sqrt[Energy (1 - y^2/Energy)];
a2[vy_, y_] := Sqrt[2 Energy (1 - (vy^2/(Energy*R^2) + y^2/Energy))]
y1 = Table[i, {i, -Sqrt[Energy], Sqrt[Energy], inc}]
vyi = Map[a1, y1];
vyf = Flatten[Range[0, vyi, (vyi - 0)/num]];
yf = Flatten[Table[#, {num + 1}] & /@ y1];
vx1 = Re[a2[a, b] /. {a -> vyf, b -> yf}]
IC = Table[{vx1[[i]], yf[[i]], vyf[[i]]}, {i, 1, (num + 1)^2}]

where a=2*Energy,b=2*Energy*R^2 and c=Energy. (vx1,yf,vyf) represents (x,y,z)

Excuse me if this sounds a very basic question, but I am new to mathematica. I am trying to learn through the documentation but I could not get a good reference on how to go about this problem.

Neo
  • 53
  • 4
  • Welcome to Mathematica.SE! I suggest that: 1) You take the introductory Tour now! 2) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! 3) As you receive help, try to give it too, by answering questions in your area of expertise. – bbgodfrey Mar 12 '15 at 16:12
  • Please provide sample code that you are using. – bbgodfrey Mar 12 '15 at 16:13
  • 1
    What does this question have to do with "zeros"? Is your question instead: "How do I randomly choose points from the surface of an ellipsoid?" – David G. Stork Mar 12 '15 at 16:16
  • @DavidG.Stork: Yes sir, I want to know a way to find out uniformly distributed random points on the surface of an ellipsoid. Kindly excuse me for the error. – Neo Mar 12 '15 at 16:25
  • See http://math.stackexchange.com/questions/973101/how-to-generate-points-uniformly-distributed-on-the-surface-of-an-ellipsoid – David G. Stork Mar 12 '15 at 16:28
  • This and more: 32501 – Kuba Mar 12 '15 at 16:44
  • 1
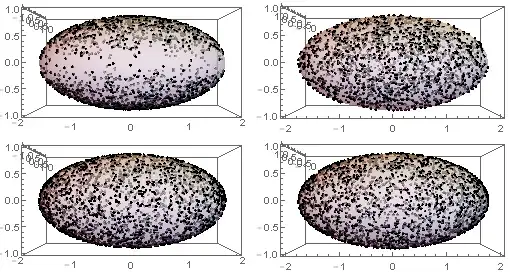
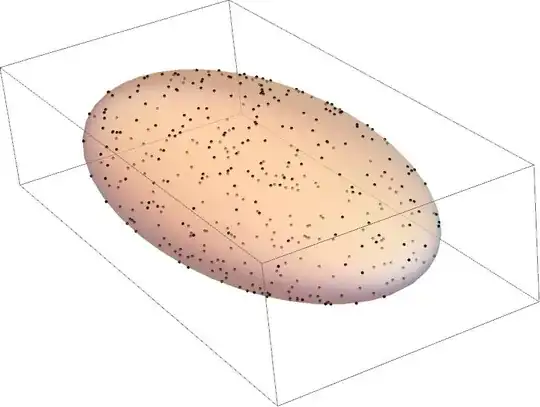
    @Kuba RandomPoint is really a killer feature of v10.2 for uniform sampling on geometric regions. – kirma Jan 07 '16 at 12:22

2 Answers2

4

You could also use this pl2 function, which does in fact distribute the points uniformly, unlike the pl function from the other answer:

lst[a_, b_, c_, n_] := Select[MapThread[{#1, #2, c RandomChoice[{-1, 1}]
  Sqrt[1 - (#1/a)^2 - (#2/b)^2]} &, {RandomReal[{-a, a}, n], 
  RandomReal[{-b, b}, n]}], #[[3]] \[Element] Reals &];

pl[a_, b_, c_, n_, v_] := Show[{Graphics3D[Point[#] & /@ lst[a, b, c, n]],
  Graphics3D[{Opacity[0.5], Ellipsoid[{0, 0, 0}, {a, b, c}]}]},
  Axes -> True, AspectRatio -> Automatic, ViewPoint -> v, ImageSize -> 250];

pl2[a_, b_, c_, n_, v_] := With[{L = RandomVariate[MultinormalDistribution[{0, 0, 0},
  DiagonalMatrix[{##}]], n]}, Show[Graphics3D[Thread[Point[(a b c)/Sqrt[(L L).{#2 #3,
  # #3, # #2}] L]]], Graphics3D[{Opacity[0.5], Ellipsoid[{0, 0, 0}, {a, b, c}]}],
  Axes -> True, AspectRatio -> Automatic, ViewPoint -> v, ImageSize -> 250]] &[a^2, b^2, c^2]

a = 3; b = 1; c = 1;
Grid[{{pl[a, b, c, #, Front], pl[a, b, c, #, Top]},
  {pl2[a, b, c, #, Front], pl2[a, b, c, #, Top]}}] &[2500]

enter image description here

With b == c the top and front view should be the "same"!

Coolwater
  • 20,257
  • 3
  • 35
  • 64
2

If I understood you right, there is a function returning n uniformly distributed random numbers lying on the ellipsoid with the surface you have specified:

        lst[a_, b_, c_, n_] := 
  Select[MapThread[{#1, #2, 
      c*RandomChoice[{-1, 1}]*
       Sqrt[1 - (#1/a)^2 - (#2/b)^2]} &, {RandomReal[{-a, a}, n], 
     RandomReal[{-b, b}, n]}], #[[3]] \[Element] Reals &];

This draws the image along with the ellipsoid in question:

 pl[a_, b_, c_, n_] := Show[{
    Graphics3D[Point[#] & /@ lst[a, b, c, n]],
    Graphics3D[{Opacity[0.5], Ellipsoid[{0, 0, 0}, {a, b, c}]}]
    }];

Let us draw them and check that they are indeed where we want them. I will choose the ellipsoid with the semi-axes 1,2 and 0.5:

pl[1, 2, 0.5, 500]

It should look as follows:

enter image description here

Have fun!

Alexei Boulbitch
  • 39,397
  • 2
  • 47
  • 96