5

Basically I want to solve Laplace equation for truncated octahedron in a cube matrix. The boundary condition is Concentration u=200 at surface of truncated octahedron and u=15 at boundary of cube. I realise there is a similar case in 2D here(Solve Laplace equation using NDSolve), but apparently I haven't understood some of the functions. Thanks a lot for helps!

TruncatedOctahedron = {x + y + z <= 10 && x + y - z <= 10 && 
x - y + z <= 10 && -x + y + z <= 10 && x + y + z >= -10 && 
x + y - z >= -10 && x - y + z >= -10 && -x + y + z >= -10 && 
-6 <= x <= 6 && -6 <= y <= 6 && -6 <= z <= 6}；
Cube = Cuboid[{-100, -100, -100}, {100, 100, 100}];
Subscript[\[CapitalGamma], D] = {DirichletCondition[u[x, y, z] == 200., 
{x, y, z} \[Element] TruncatedOctahedron], 
DirichletCondition[u[x, y, z] == 15., {x, y, z} \[Element] Cube]};
\[CapitalOmega] = RegionDifference[Cube, TruncatedOctahedron]
sol = NDSolveValue[{Inactive[Laplacian][u[x, y, z], {x, y, z}] == 0, 
Subscript[\[CapitalGamma], D]}, u, {x, y, z} \[Element] \[CapitalOmega]];
user21
  • 39,710
  • 8
  • 110
  • 167
Jack Zhang
  • 57
  • 6

1 Answers1

11

Here is a way to do it:

TruncatedOctahedron = 
  ImplicitRegion[{x + y + z <= 10 && x + y - z <= 10 && 
     x - y + z <= 10 && -x + y + z <= 10 && x + y + z >= -10 && 
     x + y - z >= -10 && 
     x - y + z >= -10 && -x + y + z >= -10 && -6 <= x <= 6 && -6 <= 
      y <= 6 && -6 <= z <= 6}, {x, y, z}];

We use exact faces to construct the boundary element mesh. For this we first make a boundary element mesh from this:

Needs["PolyhedronOperations`"]
gc = Truncate[PolyhedronData["Octahedron", "Faces"], 4/10];
gc[[1]] *= 14.14213;
dg = DiscretizeGraphics[gc];
(to = ToBoundaryMesh[dg])["Wireframe"]

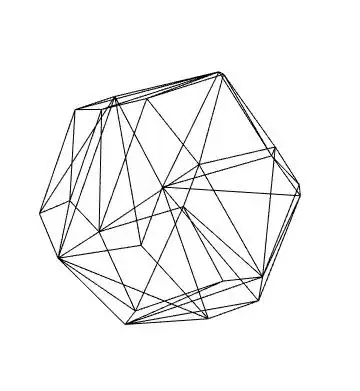
enter image description here

Next, we create the boundary element mesh and check that the truncated octahedron is matches to one you posted:

Needs["NDSolve`FEM`"]
cl = 100;
bmesh = ToBoundaryMesh[
   "Coordinates" -> 
    Join[to["Coordinates"], 
     cl*{{-1., -1., -1.}, {1., -1., -1.}, {1., 1., -1.},
       {-1., 1., -1.}, {-1., -1., 1.}, {1., -1., 1.}, {1., 1., 
        1.}, {-1., 1., 1.}}], 
   "BoundaryElements" -> 
    Join[to["BoundaryElements"], {QuadElement[
       Length[to["Coordinates"]] + {{1, 2, 3, 4}, {8, 7, 6, 5}, {1, 
          5, 6, 
             2}, {2, 6, 7, 3}, {3, 7, 8, 4}, {4, 8, 5, 1}}]}], 
   "RegionHoles" -> {{0, 0, 0}}];

Show[
 RegionPlot3D[TruncatedOctahedron],
 bmesh["Wireframe"], "PlotRange" -> {{-10, 10}, {-10, 10}, {-10, 10}}
 ]

enter image description here

In a next step we add markers to the boundary mesh. Once the full mesh is generated those will be propagated and we can use them from within NDSolve.

pointMarkerFunction = Compile[{{coords, _Real, 2}},
   Which[
      Sqrt[Total[#^2]] <= 10, 1,
      True, 2] & /@ coords];
boundaryMarkerFunction = 
  Compile[{{boundaryElementCoords, _Real, 
     3}, {pointMarkres, _Integer, 2}},
   Which[
      Union[#] === {1}, 1,
      True, 2 ] & /@ pointMarkres];
cl = 20; (* made this a bit smaller *)
bmesh = ToBoundaryMesh[
   "Coordinates" -> 
    Join[to["Coordinates"], 
     cl*{{-1., -1., -1.}, {1., -1., -1.}, {1., 1., -1.},
       {-1., 1., -1.}, {-1., -1., 1.}, {1., -1., 1.}, {1., 1., 
        1.}, {-1., 1., 1.}}], 
   "BoundaryElements" -> 
    Join[to["BoundaryElements"], {QuadElement[
       Length[to["Coordinates"]] + {{1, 2, 3, 4}, {8, 7, 6, 5}, {1, 
          5, 6, 
             2}, {2, 6, 7, 3}, {3, 7, 8, 4}, {4, 8, 5, 1}}]}], 
   "RegionHoles" -> {{0, 0, 0}}, 
   "PointMarkerFunction" -> pointMarkerFunction, 
   "BoundaryMarkerFunction" -> boundaryMarkerFunction];

We inspect the point and boundary markers:

Show[
 bmesh["Wireframe"[Boxed -> False, 
   "MeshElementStyle" -> {EdgeForm[Red], EdgeForm[Blue]}]],
 bmesh["Wireframe"[Boxed -> False, "MeshElement" -> "PointElements", 
   "MeshElementStyle" -> {Red, Blue}]]
 ]

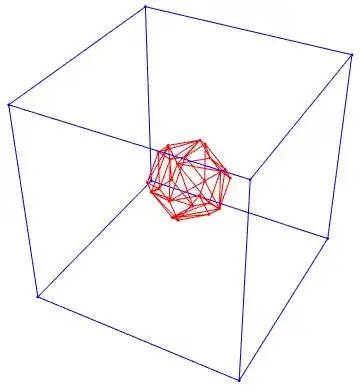
enter image description here

Create the mesh:

mesh = ToElementMesh[bmesh]

Solve the PDE:

sol = NDSolveValue[{Laplacian[u[x, y, z], {x, y, z}] == 
    0, {DirichletCondition[u[x, y, z] == 200., ElementMarker == 1], 
    DirichletCondition[u[x, y, z] == 15., ElementMarker == 2]}}, 
  u, {x, y, z} \[Element] mesh]

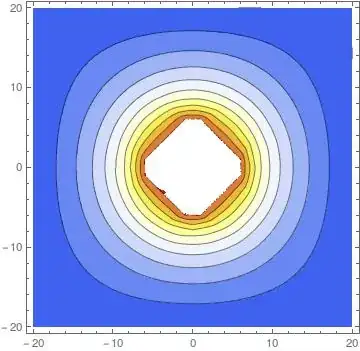
Visualize the solution:

Manipulate[
 ContourPlot[sol[x, y, z], {x, -cl, cl}, {y, -cl, cl}, 
  RegionFunction -> 
   Function[{x, y}, ElementMeshRegionMember[mesh, {x, y, z}]], 
  ColorFunction -> "TemperatureMap", 
  Contours -> Range[15, 200, (200 - 15)/10.]], {{z, 0}, -cl, cl, 1}]

More details about the mesh generation and visualization can be found here, here, here and here

enter image description here

user21
  • 39,710
  • 8
  • 110
  • 167
  • Thanks a lot for your help and such detailed explanation! It is an excellent tutorial on how to generate mesh and solve PDE. A wondering I have is why sometimes it can solve the PDE without manual mesh setting (i.e. the 2D case), but sometimes have to do so? – Jack Zhang Mar 14 '15 at 06:56
  • 1
    @JackZhang, the automatic boundary mesh generation algorithms in 3D are not yet as strong as I'd like them to be (V10.0). They work well in 1D and2D. The 3D will be improved in upcoming versions for sure. The good things is however, even if the meshing does not work as well as expected one can always go back to a manual approach. It's not ideal, but better then nothing at all, I would think. – user21 Mar 16 '15 at 09:37