3

Consider this numerical integration of Bessel function:

Do[NIntegrate[BesselJ[2, x], {x, 0, 10000}], {i, 1, 100}] // AbsoluteTiming

{4.033403, Null}

This is the similar code in Matlab:

clc
clear all;
f = @(x) besselj(2,x);

tic
for i=1:100
integral(f,0,10000);
end
toc

Elapsed time is 0.860757 seconds.

ans: 0.9964

How can I make the numerical integration in Mathematica as fast as Matlab? I want to do some minimization which involves the numerical integration of a complicated function of Bessel functions and its zeros. Mathematica calculates the zeros and the integrate slower than Matlab. I think this considerably will affect the computation speed because if Matlab is fast about 1 second then the many times of evaluation of these Bessel zeros and integrals accumulate a lot of time.

Could it be that the speed difference is due to being for faster in Matlab than Do in Mathematica?

But if someone calculates just one integral and use BesselJ[200,x] then there is a difference, or if Someone uses:

NIntegrate[BesselJ[200, x] + Sin[x], {x, 0, 30000}] // AbsoluteTiming

{2.340000, 2.593083412014634}

clc
clear all;
f = @(x)  besselj(200,x)+sin(x);
tic
integral(f,0,30000)
toc

Elapsed time is 0.264900 seconds.

ans :2.5931

I use Mathematica 9 and Matlab 2014a on Windows7.

MOON
  • 3,864
  • 23
  • 49
  • 1
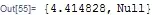
    If one omits the "Do", via NIntegrate[BesselJ[2, x], {x, 0, #}] & /@ ConstantArray[10000, 100] it is not really faster, so I do not think it is the "Do"-Loop what makes it slow. – mgamer Mar 13 '15 at 10:34
  • do they get the same result? – george2079 Mar 14 '15 at 03:24
  • @george2079 Yes, they do. – MOON Mar 14 '15 at 21:37
  • I wonder what's the output of matlab? Is it still reliable? – xzczd Mar 18 '15 at 11:31
  • @xzczd it's 0.9964 – MOON Mar 18 '15 at 11:35
  • I have a comment about your example of BesselJ[200, x] + Sin[x]. In the case where there are multi-frequency oscillations, it's easier to integrate them one by one and sum over the result. You can find NIntegrate[#, {x, 0, 30000}] & /@ (BesselJ[200, x] + Sin[x]) // AbsoluteTiming takes significantly shorter time. In general, you can first Collect different frequencies, and then NIntegrate them one by one. – Yi Wang Mar 18 '15 at 12:52
  • This speed might be influenced by Method option settings. – Daniel Lichtblau Mar 18 '15 at 15:14
  • @DanielLichtblau When I calculate the integral for a very long list in Matlab, it uses all of the CPU cores available. This is not true when I use Mathematica. You can take a look at these two questions which I think gave the same problem:

    http://mathematica.stackexchange.com/questions/77589/nintegrate-over-a-list-of-functions

    http://mathematica.stackexchange.com/questions/78278/ndsolve-in-mathematica-wont-use-all-the-cores-avaiable

     – MOON Mar 29 '15 at 11:54

1 Answers1

4
Parallelize[
  Do[NIntegrate[BesselJ[2, x], {x, 0, 10000}], {i, 1, 100}]
  ] // AbsoluteTiming

Mathematica graphics

on same PC

clc
clear all;
f = @(x) besselj(2,x);

tic
for i=1:100
integral(f,0,10000);
end
toc

 %Elapsed time is 0.924171 seconds.

Just to note, tic/toc and AbsoluteTiming measure elapsed time, not cpu time. On mutlicore, it is possible that elapsed time is smaller than CPU time. Using CPU time, the result is

Timing[Do[NIntegrate[BesselJ[2, x], {x, 0, 10000}], {i, 1, 100}]]

Mathematica graphics

While Matlab 2015a 

clc
clear all;
f = @(x) besselj(2,x);

t=cputime; 
for i=1:100
integral(f,0,10000);
end
cputime-t

%ans =
   %5.5848

So Mathematica actually used less total CPU time than Matlab. But its elapsed time was larger. It looks like Matlab used more cores (I have 8 cores). So by forcing Parallelize, Mathematica now used cores more efficiently than otherwise. That what it appears what happened, but I am not an expert on this so I could be wrong.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • so are you saying that matlab parallelisms for you? – chris Mar 13 '15 at 10:39
  • What if you would use parallelization for Matlab too? I think both cases must be either parallel or not parallel. The other thing is that if someone calculates just one integral and use BesselJ[200,x] then there is a lot of difference. – MOON Mar 13 '15 at 10:39
  • On my system if I use parallelization for Matlab, then it is faster. – MOON Mar 13 '15 at 20:06
  • @Nasser Could you use parallelization for Matlab too? I think the answer is not that Matlab uses more cores. If you use parallelization for Matlab and get the same performance as Mathematica then you're right. – MOON Mar 17 '15 at 13:43
  • @yashar Have you checked your task manager? If matlab doesn't use multi-core then the CPU utilization rate should be quite low. – xzczd Mar 18 '15 at 12:01